Într-un sistem termodinamic închis (izolat de corpuri externe), schimbarea energiei interne a oricărui corp al sistemului U1 nu poate schimba energia internă a întregului sistem. Prin urmare,
Dacă în interiorul sistemului nu funcționează niciun corp, atunci, în conformitate cu prima lege a termodinamicii, schimbarea energiei interne a oricărui corp apare numai datorită schimbului de căldură cu alte corpuri ale acestui sistem: # 916; Ui = Qi. Având în vedere. obținem:
,
Această ecuație se numește ecuația de echilibru termic. Aici Qi este cantitatea de căldură primită sau dată de corpul i. Oricare dintre cantitățile de căldură poate însemna Qi căldura generată sau absorbită în timpul topirii unui corp, ardere, evaporarea sau condensarea vaporilor, aceste procese au loc în cazul în diferite organe ale sistemului și va determina raportul adecvat.
Ecuația echilibrului termic este o expresie matematică a legii privind conservarea energiei pentru schimbul de căldură.
Lucrați în extinderea gazului
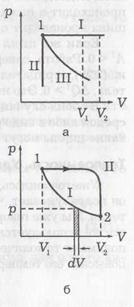
1 / V (vezi ecuația (4)). Extinderea, gazul produce munca. Să presupunem că, în cilindru, pistonul S este deplasat de o forță constantă F datorită dilatării gazului cu o distanță dx. Activitatea gazului va fi:
Dacă F se schimbă, atunci: (21).
În figura B, p # 903; dV este zona benzii umflate și a este suma suprafețelor tuturor benzilor de la V1 la V2. T. despre. Lucrarea cu gaz este măsurată cu ajutorul ariei de sub curbă din diagrama p -V. Evident, ra-bot depinde de procesul, adică. E. Matter dacă expansiunea gazului are loc de-a lungul curbei I și curba II (văzută în fig. B, sub zona curba II mai mare decât sub curba I).
În procesul izobaric (figura a, curba I), activitatea gazului:
Când procesul de izocoră (Fig. A. Curba II) volumul nu se schimbă, adică. E. DV = 0 și, în consecință, telno, A = 0. modificarea proceselor izoterme și p. și V (figura b). Înlocuirea presiunii prin volum și temperatură, conform ecuației (4), obținem lucrarea gazului la T = const:
Executăm procesul de extindere a gazului de la starea 1 (figura b) la starea 2 de-a lungul curbei II (A> 0), și comprimarea înapoi în starea 1 - de-a lungul curbei I (A<0 ). Процесс с возвращением в ту же точку называется цик-лом. Тогда общая работа будет равна разности площадей под кривыми II и I, т. е. пло-щади цикла.
Dacă ciclul pe diagramele -V p făcut în sens orar-ke (vezi. Fig. B), funcționarea expansiune este mai mare decât compresie și finaliza lucrările A> 0. Din moment ce suntem înapoi la același punct, # 916; U = 0. Rezultă din (18) că pentru un astfel de proces transferul de căldură către corp trebuie să fie mai mare decât zero (Q> 0). Acest lucru se întâmplă într-un motor termic, când este furnizat căldură, iar ma-bus-ul produce o muncă pozitivă.
Dacă ciclul se face în sens contrar acelor de ceasornic, atunci A <0. Соответственно и Q <0, т. е. энергия не подводится к телу, а отводится от него. Это имеет место в холодильнике.
În ambele cazuri, energia este schimbată cu mediul fie sub formă de muncă, fie sub formă de schimb de căldură.
Capacitatea de căldură este cantitatea de căldură care trebuie raportată sistemului pentru a crește temperatura cu 1 (K) în absența unei lucrări utile și a constanței parametrilor relevanți.
Dacă luăm o substanță individuală ca sistem, atunci capacitatea totală de căldură a sistemului este egală cu capacitatea de căldură de 1 mol de substanță () înmulțită cu numărul de moli ().
Căldura specifică poate fi specifică și molară.
Căldura specifică este cantitatea de căldură necesară pentru a încălzi o unitate de masă de materie pe 1 grad (valoare intensivă).
Capacitatea de căldură molară este cantitatea de căldură necesară pentru a încălzi un mol de material pe 1 grad.
Există o capacitate de căldură reală și medie.
În tehnologie, conceptul de capacitate medie de căldură este de obicei utilizat.
Media este capacitatea de căldură pentru un anumit interval de temperatură.
Dacă un sistem conține o cantitate de substanță sau masă. a raportat cantitatea de căldură. iar temperatura sistemului a crescut de la. atunci capacitatea medie termică specifică sau molară poate fi calculată:
Capacitatea reală de căldură molară este raportul dintre cantitatea infinită de căldură împărțită de 1 mol de substanță la o anumită temperatură și creșterea temperaturii, care se observă în acest caz.
Conform Eq. (19), capacitatea de căldură, ca și căldura, nu este o funcție a statului. La presiune constantă sau volum, în conformitate cu ecuațiile (11) și (12), căldură și capaitatii termică și dobândesc proprietățile funcției de stat, adică sunt funcții caracteristice ale sistemului. Astfel, obținem capacități de încălzire izocoric și izobaric.
Capacitatea de căldură izocorică este cantitatea de căldură care trebuie raportată sistemului în scopul creșterii temperaturii cu 1. dacă procesul are loc la.
Capacitatea termică izobarică este cantitatea de căldură care trebuie raportată sistemului pentru a crește temperatura cu 1 la.
Capacitatea de căldură nu depinde numai de temperatura, ci și asupra volumului sistemului, deoarece există forțele de interacțiune între particule, care este modificat prin schimbarea distanței dintre ele, însă în ecuațiile (20) și (21) folosind derivatele parțiale.
Entalpia unui gaz ideal, la fel ca energia sa internă, este doar o funcție a temperaturii:
dar în concordanță cu ecuația lui Mendeleev-Clapeyron. atunci
Prin urmare, pentru un gaz ideal în ecuațiile (20), (21), derivații parțiali pot fi înlocuiți cu diferențele totale:
Din soluția comună a ecuațiilor (23) și (24) cu rezonanță pentru (22), obținem ecuația relației dintre și pentru un gaz ideal.
Împărțind variabilele în ecuațiile (23) și (24), putem calcula schimbarea energiei interne și a entalpiei când 1 mol de gaz ideal este încălzit de la temperatură la
Dacă în domeniul de temperatură indicat capacitatea de căldură poate fi considerată constantă, atunci în urma integrării obținem:
Noi stabilim relația dintre capacitatea medie și cea reală de căldură. Schimbarea entropiei pe de o parte este exprimată prin ecuația (27), pe de altă parte -
Ecuând părțile drepte ale ecuațiilor și exprimând capacitatea medie de căldură, avem:
O expresie similară poate fi obținută pentru capacitatea medie de încălzire izocorică.
Capacitatea de căldură a majorității substanțelor solide, lichide și gazoase crește odată cu creșterea temperaturii. Dependența capacității de căldură a substanțelor solide, lichide și gazoase la temperatură este exprimată printr-o ecuație empirică de formă:
unde a. b. c și - coeficienți empirici, calculată pe baza datelor experimentale privind. coeficientul se referă la substanțele organice și - la anorganici. Valorile coeficienților pentru diferite substanțe sunt prezentate în manual și sunt aplicabile numai pentru intervalul de temperatură specificat.
Căldura specifică a unui gaz ideal nu depinde de temperatură. Conform teoriei moleculare-cinetice, capacitatea de căldură pe un grad de libertate este egală cu (gradul de libertate - numărul de tipuri de mișcări independente în care mișcarea complexă a unei molecule poate fi descompusă). Pentru o moleculă monatomică, mișcarea de translație este caracteristică, care poate fi descompusă în trei componente în conformitate cu trei direcții reciproc perpendiculare de-a lungul celor trei axe. Prin urmare, capacitatea de încălzire izochorică a unui gaz ideal monatomic este
Apoi, capacitatea de căldură izobarică a gazului ideal monatomic, conform (25), este determinată prin ecuație
Moleculele diatomice ale unui gaz ideal au în plus față de trei grade de libertate a mișcării de translație și 2 grade de libertate de mișcare de rotație. Prin urmare: