§ 71 DIFFICAȚIA LUMINII
Dacă lumina este un proces val, împreună cu interferența trebuie respectate și difracția luminii. La urma urmei, difracția - îndoirea de către valurile marginilor obstacolelor - este inerentă în orice mișcare a undelor. Dar observa difracția luminii nu este ușor, deoarece valurile sunt deviate de la propagarea rectilinie la colțuri marcate numai obstacole a căror dimensiune este comparabilă cu lungimea de undă, și lungimea de undă a luminii, după cum știm de la tine este foarte mic.
Trecând printr-o mică gaură o lumină subțire de lumină, se poate observa o încălcare a legii propagării rectilinii a luminii. Punctul luminos de pe ecran față de gaură va fi mai mare decât dimensiunea fasciculului.
Experiența lui Jung. În 1802, T. Jung, care a descoperit interferența luminii, a pus experimentul clasic pe difracție (Figura 8.55). Într-un ecran opac, el a străpuns două găuri mici B și C cu un bolț la o distanță scurtă una de cealaltă. Aceste găuri au fost iluminate de un fascicul de lumină îngustă care trece printr-o mică deschidere A într-un alt ecran. A fost acest detaliu, cu care a fost foarte greu să vină la acel moment, a decis succesul experimentului. Numai valurile coerente intervin. Valul sferic rezultat din deschiderea A excitat în conformitate cu principiul Huygens a provocat oscilații coerente în găurile B și C. Datorită difracției din găurile B și C, au apărut două conuri luminoase care s-au suprapus parțial. Ca urmare a interferenței acestor două unde luminoase, pe ecran au apărut benzi alternante de lumină și întunecate. Închiderea unuia dintre găuri. Jung a constatat că marginile de interferență au dispărut. Cu ajutorul acestui experiment, pentru prima dată, Jung a măsurat lungimile de undă corespunzătoare razelor de lumină de diferite culori și foarte precis.
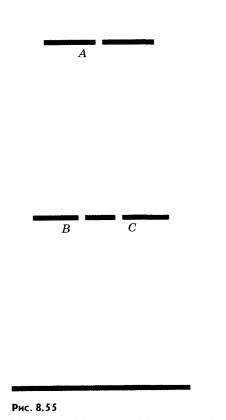
Teoria lui Fresnel. Studiul de difracție a fost finalizat în lucrările lui O. Fresnel. Frenel nu numai că a studiat mai detaliat diferitele cazuri de difracție prin experiment, dar și a dezvoltat o teorie cantitativă a difracției, care, în principiu, 8.55 Calculați modelul de difracție care apare atunci când lumina este obstrucționată de orice obstacol. De asemenea, el a explicat pentru prima dată propagarea rectilinie a luminii într-un mediu omogen pe baza teoriei undelor.
Aceste succese obținute de Frenel, combinând principiul Huygens cu ideea de interferență a undelor secundare. Conform ideii lui Fresnel, fiecare punct din frontul undei este o sursă de valuri secundare, iar toate sursele secundare sunt coerente (principiul Huens Fresnel).
Pentru a calcula amplitudinea unei unde luminoase în orice punct al spațiului, trebuie să înconjoară mental sursa de lumină cu o suprafață închisă. Interferența undelor de la sursele secundare situate pe această suprafață determină amplitudinea în punctul spațiului în cauză.
Astfel de calcule au făcut posibilă înțelegerea modului în care lumina dintr-o sursă punctuală S care emite valuri sferice atinge un punct arbitrar B al spațiului (Figura 8.56).

Fresnel Augustin (1788-1827) este un fizician francez. El a pus bazele opticii undelor. După ce a completat principiul Huygens cu ideea de interferență a undelor secundare, el a dezvoltat o teorie cantitativă a difracției. Bazat pe acest principiu, el a explicat legile opticii geometrice. în special, natura liniară a propagării luminii într-un mediu omogen. El a creat o metodă aproximativă pentru calculul modelului de difracție, pe baza separării suprafeței undei în zone. Pentru prima dată a demonstrat transversalitatea undelor luminoase.
Dacă luăm în considerare sursele secundare pe o suprafață sferică val rază R, rezultatul undelor de interferență din aceste surse secundare de la punctul B este aceeași ca și în cazul în care numai surse secundare de mici segment sferic ab trimiterea luminii la punctul B. Undele secundare emise de surse dispuse la restul suprafeței, se anulează reciproc din cauza interferențelor. Prin urmare, totul se întâmplă ca și în cazul în care lumina propagată de-a lungul liniei SB, T. E. Într-o linie dreaptă.
Pe baza acestei teorii, Fresnel a demonstrat caracterul direct al propagării luminii și difracția cantitativă considerată pe diferite tipuri de obstacole.
Modelele de difracție din diferite obstacole. Calculele efectuate de Fresnel au fost pe deplin confirmate prin experiment. Deoarece lungimea undei de lumină este foarte mică, unghiul de deviere a luminii de la direcția propagării rectilinii este mic. Prin urmare, pentru o observație distinctă a difracției, trebuie fie să utilizați obstacole foarte mici, fie să nu amplasați ecranul departe de obstacole. Dacă distanța dintre obstacol și ecran este de ordinul unui contor, dimensiunile obstacolului nu trebuie să depășească sute de milimetri. Dacă distanța până la ecran atinge sute de metri sau câțiva kilometri, difracția poate fi observată pe obstacole de câțiva centimetri și chiar metri în dimensiune.
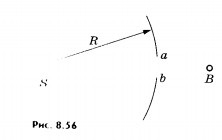
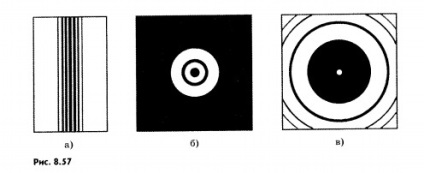
Figura 8.57, a-c prezintă schematic modele de difracție din diferite obstacole: a - dintr-un fir subțire; b - din gaura rotunda; în - din ecranul rotund.
În locul unei umbre din fir, dungile luminoase și întunecate sunt vizibile; în centrul modelului de difracție, apare un punct întunecat din gaură, înconjurat de inele luminoase și întunecate 1; În centrul umbrei formate de un ecran rotund, este vizibil un punct luminos, iar umbra însăși este înconjurată de inele concentrice întunecate.
Un incident curios a avut loc la o reuniune a Academiei Franceze de Științe, în 1818. Unul dintre oamenii de știință care au participat la reuniune, a subliniat că teoria Fresnel urmează faptelor în mod evident contrare bunului simț. Astfel, pentru anumite dimensiuni ale orificiilor și la anumite distanțe de la gaură până la sursa de lumină și ecranul, trebuie să existe o specie întunecată în centrul punctului luminos. Și în spatele unui mic disc opac, dimpotrivă, ar trebui să existe un loc luminos în centrul umbrei. Care a fost surpriza oamenilor de stiinta cand experimentele s-au dovedit a fi adevarat!
Limitele aplicabilității optice geometrice. Toate teoriile fizice reflectă procesele care se produc în natură doar aproximativ. Pentru orice teorie, anumite limite ale aplicabilității sale pot fi indicate. Indiferent dacă este posibil să se aplice această teorie într-un caz particular sau nu, depinde nu numai de precizia pe care o oferă această teorie, ci și de acuratețea necesară pentru rezolvarea unei probleme practice date. Limitele aplicabilității teoriei pot fi stabilite numai după ce a fost elaborată o teorie mai generală care să acopere aceleași fenomene.
Toate aceste dispoziții generale se aplică la optica geometrică. Această teorie este aproximativă. Nu poate explica, de exemplu, fenomenele de interferență și de difracție a luminii. O teorie mai generală și mai precisă este optica undelor. Potrivit acesteia, legea propagării rectilinii a luminii și a altor legi ale opțiunii geometrice se realizează destul de precis dacă dimensiunile obstacolelor din calea propagării luminii sunt mult mai mari decât lungimea de undă a undei luminoase. Dar ele nu sunt îndeplinite.
1 Schimbând diametrul găurii, puteți obține un punct luminos în centrul modelului de difracție, înconjurat de inele întunecate și luminoase.
Acțiunea dispozitivelor optice este descrisă de legile opticii geometrice. Conform acestor legi, este posibil să se facă distincția, cu ajutorul unui microscop, a unor detalii arbitrare despre obiect; Folosind telescopul, este posibil să se stabilească existența a două stele pentru orice distanțe unghiulare mici între ele. Cu toate acestea, în realitate, acest lucru nu este valabil și numai teoria undelor luminoase face posibilă înțelegerea motivelor pentru limita de rezoluție a instrumentelor optice.
Rezoluția microscopului și a telescopului. Natura lumină a luminii impune o limită a capacității de a distinge detaliile unui obiect sau obiecte foarte mici atunci când sunt observate cu ajutorul unui microscop. Difracția nu face posibilă obținerea unor imagini distincte ale obiectelor mici, deoarece lumina nu se propagă strict rectiliniu, ci învelințează obiecte. Din acest motiv, imaginile sunt neclare. Aceasta se întâmplă atunci când dimensiunile liniare ale obiectelor sunt mai mici decât lungimea undei luminoase.
Difracția impune de asemenea o limită a puterii de rezolvare a telescopului. Datorită difracției valurilor de lângă marginea jantei, imaginea stelei nu va fi un punct, ci un sistem de inele luminoase și întunecate. Dacă două stele se află la o distanță unghiulară mică una de cealaltă, aceste inele sunt suprapuse între ele și ochiul nu poate distinge dacă există două puncte luminoase sau una. Distanta unghiulara limita dintre punctele luminoase la care pot fi distingate este determinata de raportul dintre lungimea de unda si diametrul obiectivului.
Acest exemplu arată că, prin difracție, este necesar să fie luată în considerare întotdeauna, la orice obstacol. Nu poate fi neglijată cu observații foarte atente chiar și în cazul unor obstacole a căror dimensiuni sunt mult mai mari decât lungimea de undă.
Difracția luminii determină limitele aplicabilității optice geometrice. Obstacolele de încovoiere a luminii plasează o limită a rezoluției celor mai importante instrumente optice - un telescop și un microscop.
1. Ce fenomen se numește difracție!
2. De ce difracția undelor mecanice este mai ușor de observat decât difracția luminii!
3. De ce nu puteți vedea un atom cu un microscop!
4. În ce cazuri sunt legile opticii geometrice aproximativ valabile?
Manualul de descărcare a tuturor subiecților. dezvoltarea de planuri de lecții pentru profesori, fizică și astronomie pentru clasa a 11-a on-line
Dacă aveți corecții sau sugestii pentru această lecție, scrieți-ne.
Dacă doriți să vedeți alte ajustări și dorințe pentru lecții, consultați aici - Forumul educațional.