Pentru a rezolva problemele de geometrie, este necesar să se cunoască cu formula - cum ar fi aria unui triunghi sau o zonă paralelogram - precum și tehnici simple, pe care le descrie.
În primul rând, să învățăm formulele din zonele cifrelor. Le-am colectat special într-o masă convenabilă. Imprimați, învățați și aplicați!
Desigur, nu toate formulele de geometrie sunt în tabelul nostru. De exemplu, pentru a rezolva problema C4, în a doua parte a UTI se aplică alte formule din zona triunghiului. Vom spune despre ei.
Și dacă nu trebuie să găsești zona unui trapez sau a unui triunghi, ci zona unei figuri complexe? Există căi universale! Să le arătăm exemplele de la banca sarcinilor FIPI.
Cum de a găsi zona de figura non-standard? De exemplu, un quadrilateral arbitrar? O tehnică simplă este de a sparge această figură în cele pe care le cunoaștem cu toții și de a găsi suprafața ei ca sumă a zonelor acestor cifre.
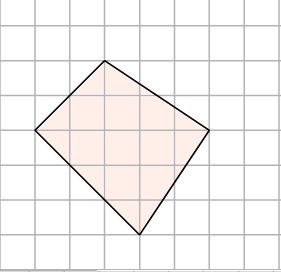
Împărțim acest patrulater cu o linie orizontală în două triunghiuri cu o bază comună egală cu. Înălțimile acestor triunghiuri sunt egale cu și. Apoi, suprafața patrulaterului este egală cu suma zonelor a două triunghiuri :.
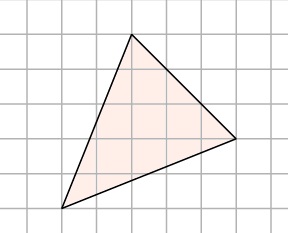
În unele cazuri, aria figurii poate fi reprezentat ca diferența de orice ploschadey.Ne atât de ușor de găsit, care sunt baza și înălțimea triunghiului! Dar putem spune că zona este egală cu diferența dintre suprafața unui pătrat cu latura și trei triunghiuri drepte. Le vedeți în imagine? Obținerea: /
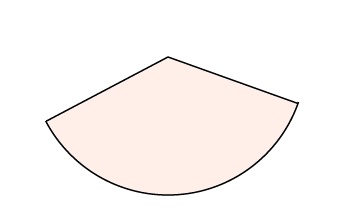
Uneori în sarcină este necesar să găsim zona nu a întregii figuri, ci părți ale acesteia. De obicei, este vorba despre zone ale sectorului - zona sectorului kruga.Naydite parte dintr-un cerc de rază, lungimea arcului este egală .Pe această cifră, vom vedea o parte a cercului. Zona întregului cerc este egală, deoarece. Rămâne să aflăm care parte a cercului este descrisă. Deoarece lungimea întreaga circumferință este egală cu (pentru) și, prin urmare, lungimea de arc a sectorului este de ori lungimea arcului tt mai mică decât lungimea întregii circumferințe. Unghiul la care se sprijină acest arc este de asemenea o fracțiune a cercului complet (adică grade). Astfel, zona sectorului va fi ori mai mică decât a întregului cerc.