Suma a + b a doi vectori a și b este un vector care merge de la începutul până la sfârșitul vectorului și vectorul b cu condiția ca vectorul b este atașat la capătul unui vector (de obicei, un triunghi) Construirea unei sume + b este prezentat în Fig. 42.
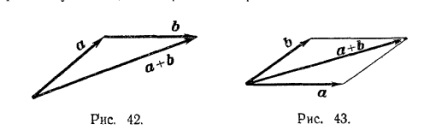
În plus față de regula triunghiului este adesea folosit (echivalent cu acesta). regula paralelogramului: dacă vectorii a și b sunt date la originea comună și au construit un paralelogram, atunci suma a + b este un vector care coincide cu o diagonală a acestei paralelogramului se extinde de la o origine comună și și b (Figura 43.). Urmează imediat că a + b = b + a.
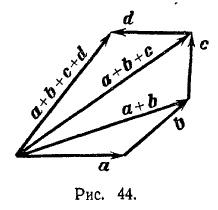
Adăugarea multor vectori se face prin aplicarea succesivă a regulii triunghiului (vezi figura 44, unde este prezentată construcția sumelor a patru vectori a, b, c, d).
Diferența dintre a - b a doi vectori a și b este un vector care este suma și UI cu vectorul b este un vector. Dacă cei doi vectori a și b sunt date la originea comună, diferența a - b este un vector care se extinde din capătul b ( „scăzute“) și capătul ( „descăzut“). Doi vectori de lungime egală, care se află pe o linie dreaptă și îndreptate în direcții opuse, se numesc reciproc inverse: dacă una dintre ele este marcat cu un, celălalt este notat cu s. Este ușor de observat că a = b = a + (-b). Astfel, construcția este echivalentă cu adăugarea unei diferențe „scade“ inversa vectorul „scăzută“.
Produsul om (sau, de asemenea, aα) al unui număr α este un vector al cărui modul este egal cu produsul modulului a prin modulul α; este paralel cu vectorul a sau se află pe acesta pe o singură linie și este direcționat în același mod ca vectorul a, dacă α este un număr pozitiv și este opus vectorului a dacă α este un număr negativ.
Adăugarea de vectori și înmulțirea unui vector cu un număr se numesc operații liniare pe vectori.
Următoarele două teoreme de bază privind proiecțiile vectorilor sunt:
1. Proiecția sumei vectorilor pe o axă este egală cu suma proeminențelor lor pe aceeași axă:
2. Când vectorul este înmulțit cu un număr, proiecția sa este înmulțită "și același număr:
În special, dacă
Dacă a = (X; Y; Z), atunci pentru orice număr α
Vectorii situați pe o linie sau pe linii paralele sunt numiți coliniari. Un semn al colinearității a doi vectori
este proporționalitatea coordonatelor lor:
Un triple de vectori i, j, k se numește o bază de coordonate dacă acești vectori îndeplinesc următoarele condiții:
1) vectorul i se află pe axa Ox, vectorul i pe axa Oy, vectorul k pe axa Oz;
2) fiecare dintre vectorii i, j, k este direcționat pe axa sa într-o direcție pozitivă;
3) vectorii i, j, k sunt vectori unici, adică, | i | = 1, | j = 1, | k | = 1
Indiferent de vectorul a, acesta poate fi întotdeauna extins în termeni de bază i, j, k, adică poate fi reprezentat ca:
coeficienții acestei extinderi sunt coordonatele vectorului a (adică, X, Y, Z sunt proiecțiile vectorului a pe axele coordonatelor).
761. Având în vedere vectorii a și b, construiți fiecare vector următor: 1) a + b; 2) a-b; 3) b - a; 4) -a-b.
762. Având în vedere: | a | = 13, | b | = 19 și | a + b | = 24. Calculați | a - b |.
763. Având în vedere: | a. | = 11, | b | = 23 și | a - b | = 30. Determinați | a + b |.
764. Vectorii a și b sunt reciproc perpendiculari, și | a | = 5 și | b | = 12. Definiți | a + b | și | a - b |.
765. Vectorii a și b formează un unghi φ = 60 °, și | a | = 5 și | b | = 8. Definiți | a + b | și | a - b |.
766. Vectorii a și b formează un unghi φ = 120 °, unde | a | = 3 și | 6 | = 5. Definiți | a + b | și | a - b |.
767. Ce condiție trebuie să îndeplinească vectorii a și b, pentru a avea următoarele relații: 1) | a + b | = | a-b |; 2) | a + b |> | a-b |; 3) | a + b |