Fulgii de zăpadă au simetrie Dih6 dihedral, la fel ca hexagonul obișnuit.
Grupul dihedral (grup dihedral) este grupul de simetrie al unui poligon obișnuit. care include ambele rotații. și simetrii axiale [1]. Grupurile diridice sunt cele mai simple exemple de grupuri finite și joacă un rol important în teoria grupurilor. geometrie și chimie. Este bine cunoscut și complet trivial să se verifice că grupul format din două involuții cu un număr finit de elemente în domeniul definiției este un grup dihedral.
Notatii [ ]
Există două tipuri principale de înregistrare a unui grup dihedral asociat cu un poligon n-lateral. În geometrie, grupul este scris ca Dn. în timp ce în algebra generală același grup este notat ca D2n. folosind ca index un număr de elemente din grup. Există și notația Coxeter. în care simetria axială este notată ca [n] (de ordine 2n) și rotația ca [n] + (a ordinului n). Un alt record este notația de orație. în care simetria axială este notată cu * nn. și rotații ca n.
În acest articol, Dn (sau, uneori, Dihn) se referă la simetriile unui regulat n-gon.
Definiție [ ]
Elemente [ ]
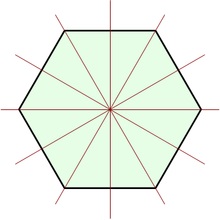
Șase reflecții axiale ale unui hexagon regulat
Un regulat n -gon are 2n simetrii diferite: n rotații și n reflecții axiale. care formează grupul dihedral Dn. Dacă n este ciudat, fiecare axă de simetrie trece prin mijlocul unei părți și pe vârful opus. Dacă n este egal, există n / 2 axe de simetrie care conectează punctele medii ale laturilor opuse și n / 2 axe care leagă vârfurile opuse. În orice caz, există n axele de simetrie și elementele 2n din grupul de simetrie. Reflecția asupra unei axe și apoi a celeilalte, duce la rotirea la un unghi dublu între axe. Imaginile de mai jos arată rezultatul acțiunii elementului D8 pe semnul rutier Stop:

Prima linie prezintă opt rotații, iar cea de-a doua - opt reflecții.
Structura grupului [ ]
În ceea ce privește orice alt obiect geometric, compoziția a două simetrii ale unui poligon regulat va fi din nou o simetrie. Astfel, simetriile unui poligon regulat formează un grup finit.
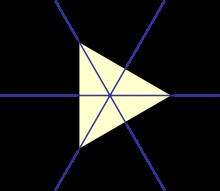
Grupul dihedral ca grup de simetrie în 2D și grupul de rotație în 3D [ ]
Un exemplu al grupului abstract Dihn și calea convențională a reprezentării grafice este grupul Dn al izometriei planului. nu mutați originea. Aceste grupuri formează una din cele două serii de grupuri discrete de puncte pe un avion. Dn constă în rotații n cu un unghi multiplu de 360 ° / n. în jurul originii coordonatelor și reflecții cu privire la axele n care trec prin centrul coordonatelor și un unghi față de axele rămase, un multiplu de 180 ° / n. Aceste puncte reprezintă grupul de simetrie al unui poligon obișnuit cu n laturi (pentru n ≥ 3).
Grupul dihedral Dnis este generat de o rotație r a ordinului n și o reflexie a ordinii 2, astfel încât
În ceea ce privește geometria: imaginea oglindă a rotației arată ca o rotație inversă.
În ceea ce privește matricile:
grupa diedru D2 r generat de rotația de 180 de grade, iar axa de simetrie s în raport cu X. Elementele D2 pot fi exprimate ca e, r, s, rs>, unde e - transformarea identității și rs - simetrie în raport cu axa Y.
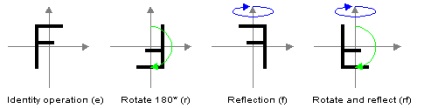
Patru elemente ale lui D2 (aici axa X este verticală)
Pentru n> 2, operațiile de rotație și reflexie față de o linie dreaptă nu sunt comutative și Dn nu este abeliană. De exemplu, în D4. rotație de 90 de grade, iar apoi reflexia dă un rezultat complet diferit de reflecție și apoi de rotație.
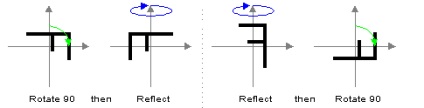
D4 nu este Abelian (axa X este aici verticală).
Astfel, odată cu aplicarea evidentă la probleme în planul de simetrie, aceste grupuri sunt simple exemple de grupări non-Abeliene și sunt frecvent utilizate ca contra-exemple pentru teoremele limitate grupuri abeliene.
Elementele 2n ale lui Dn pot fi scrise ca e. r. r 2, ..., rn-1. s. r s. r 2 s, ..., rn -1 s. Primele n elemente listate sunt rotații, restul n sunt reflexii relative la axe (toate sunt de ordin 2). Rezultatul a două rotații sau două reflecții va fi rotația. Rezultatul rotirii și reflexiei va fi o reflecție.
Cu toate acestea, nota Dn este utilizată pentru subgrupurile SO (3). care sunt, de asemenea, grupuri de tip Dihn. grupul de simetrie al unui poligon încorporat într-un spațiu tridimensional (dacă n ≥ 3). Astfel de figuri pot fi înțelese ca și corpuri degenerate (de aici numele dihedron (dihedron)).
Exemple de simetrie a copacilor bidimensionali dihedral [ ]
Definiții echivalente [ ]
Următoarele definiții ale lui Dihn sunt echivalente:
- Grupul de automorfism al unui grafic constă doar dintr-un ciclu cu n noduri (dacă n ≥ 3).
- Un grup cu o prezentare
Proprietăți [ ]
Proprietățile grupurilor Dihn dihedral cu n ≥ 3 depind de paritatea lui n. De exemplu, centrul grupului Dihn constă doar în identitatea pentru n n. și din două elemente pentru egal, și anume, de identitate și rn / 2
Dacă m divide n. atunci Dihn are n / m subgrupuri de forma Dihm. și un subgrup Zm. Astfel, numărul total al subgrupele Dihn (n ≥ 1) este d (n) + σ (n), unde d (n) - numărul σ naturale și n divizori (n) - cantitatea de divizorilor naturale n.
Conjugarea clasei de reflecție [ ]
Toate reflecție conjugat Pairwise în cazul n impar. dar ele sunt împărțite în două clase de conjugare pentru chiar n. În ceea ce privește izomorfism -gons corecte n: impar n orice pereche de reflexii pot fi reprezentate ca rotație, în timp ce pentru chiar n doar jumătate din reflexii pot fi obținute dintr-o rotație se transformă. Din punct de vedere geometric, fiecare poligon în axa de simetrie impare trece printr-una dintre nodurile și centrul laturii opuse, iar în seara există două seturi de axe, fiecare set corespunzând conjugarea lor de clasă - axa care se extinde prin apexul și o axă care trece prin punctele mediane ale laturilor.
Algebric, este reprezentanții conjugare a teoremei lui Sylow. pentru reflecție nui n orice, împreună cu elementul de identificare al unui subgrup de ordinul 2, care este 2-Sylow subgrup (2 = 2 1> - putere maximă de doi, împărțind 2 n = 2 (2 k + 1)), în timp ce pentru chiar n . Aceste subgrupuri de ordin 2 nu sunt Sylow ca 4 (cea mai mare putere a doua) divide ordinul grupului.
Pentru un even n, în schimb, există un automorphism exterior. permițând două tipuri de reflecții.
Grupuri de automomorfisme [ ]
Acest lucru poate fi înțeles în termeni de generator de reflexie și de rotații elementare (rotații pe k (2 # x03C0; / n). pentru k este coprime cu n). Ce automorfism va fi intern și care este un automorfism exterior depinde de paritatea lui n.
- Pentru un nd n, grupul dihedral nu are nici un centru, astfel încât orice element să definească un automorfism interior netrivial. Pentru chiar n, rotația cu 180 ° (reflecție față de centrul de coordonate) este un element netrivial al centrului.
- Astfel, pentru n. grupul de automorfism interior este de ordin 2n, iar pentru cel unu, este de ordinul n.
- Pentru ciudat n. toate reflexiile sunt conjugate, chiar și ele sunt împărțite în două clase (cele care trec prin cele două vârfuri, iar cei care trec prin punctele mediane ale laturilor), iar aceste două clase sunt asociate cu un automorphism exterior, care poate fi reprezentat ca rotație # x03C0; / n (jumătate din unghiul de rotație minimă).
- Rotațiile dau un subgrup normal. Conjugarea reflecției schimbă semnul (direcția) rotației, dar în caz contrar ele nu se schimbă. Un automorfism care multiplică unghiurile cu k (care este relativ prime la n) este extern, cu excepția cazului k = # x00B1; 1.
Exemple de automorfism al grupurilor [ ]
Dih9 are 18 automorfisme interne. Ca grup de izometrii de spațiu bidimensional, D9 are reflexii cu un interval de 20 °. 18 automomorfisme interne asigură că reflexiile se rotesc cu un număr care este un multiplu de 20 ° și cu reflexii. Ca grupuri izometrice, toate sunt automorfisme. Există, în plus, 36 de automorfisme externe. de exemplu, prin înmulțirea unghiului de rotație cu 2.
Generalizări [ ]
Există mai multe generalizări importante ale grupurilor dihedral:
- Un grup dihedral infinit este un grup infinit cu o structură algebrică asemănătoare cu structura grupurilor finite dihedral. Acesta poate fi considerat un grup de simetrii de numere întregi.
- Grupul ortogonal O (2), adică grupul de simetrie al cercului. are proprietăți similare cu proprietățile grupurilor diridate finite
- Familia de grupuri dihedral generalizate include extensiile menționate mai sus, ca multe altele.
- Grupurile cuanistice sunt familii de grupuri finite cu proprietăți similare cu cele ale grupurilor diridate finite.
Consultați de asemenea [ ]
Notă [ ]
Referințe [ ]
Pentru a îmbunătăți acest articol cu privire la matematică, este de dorit: