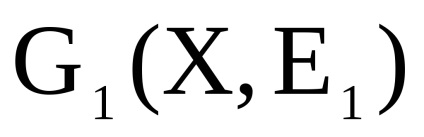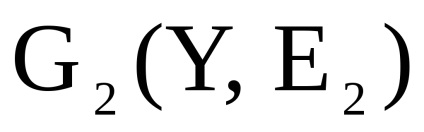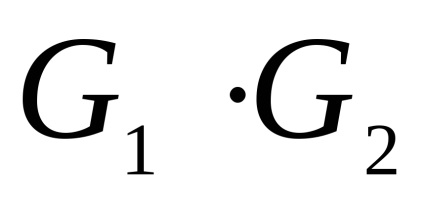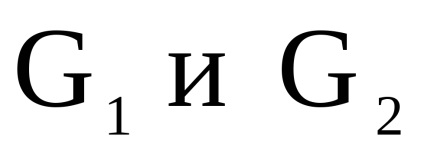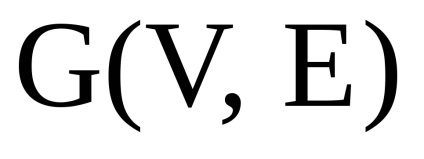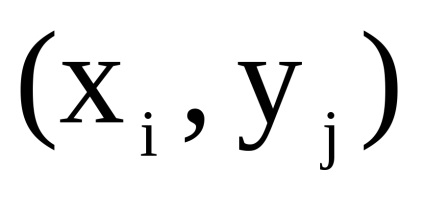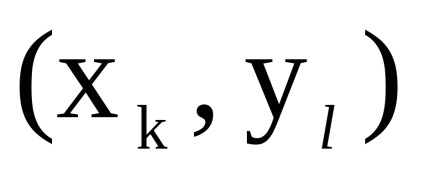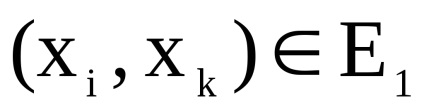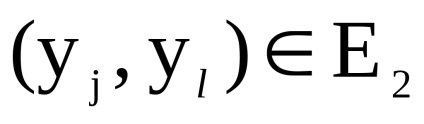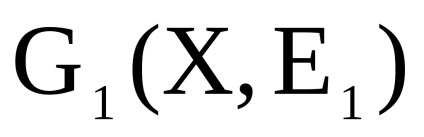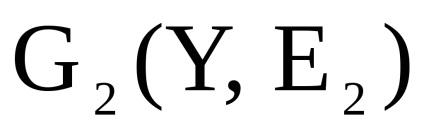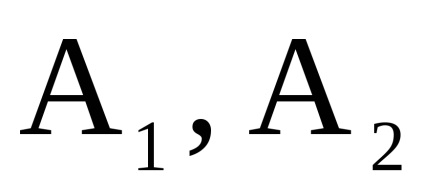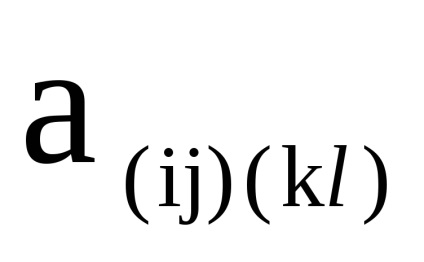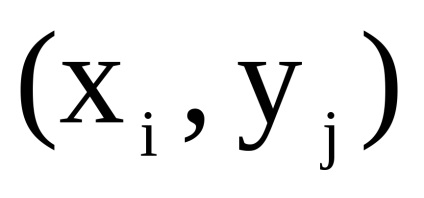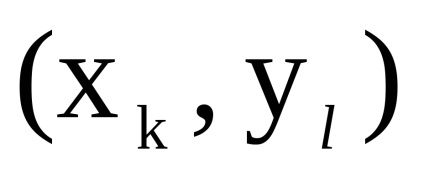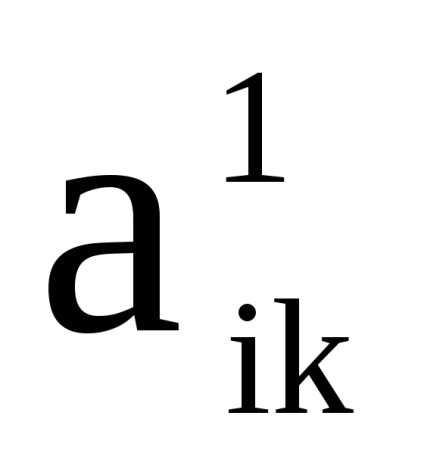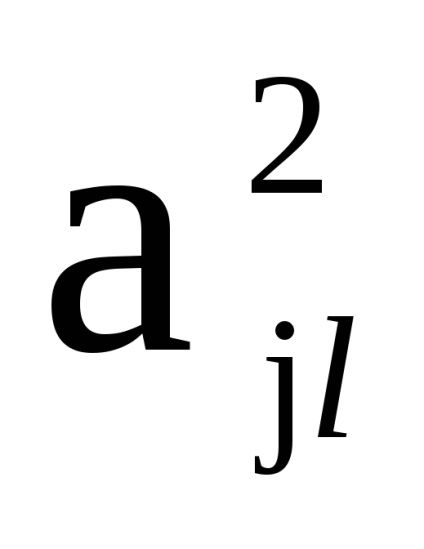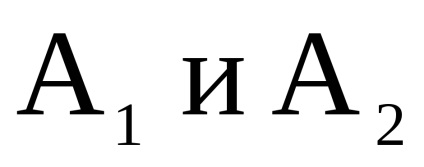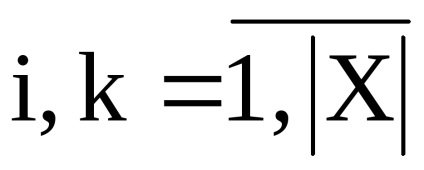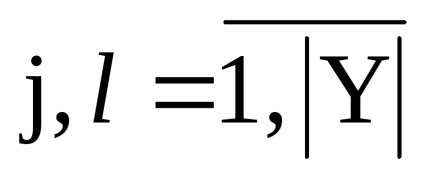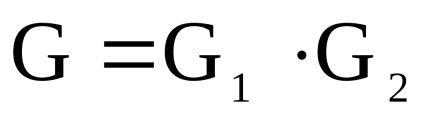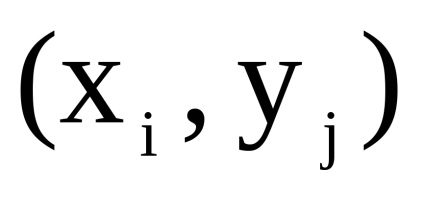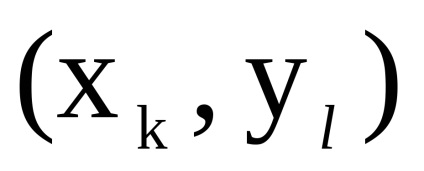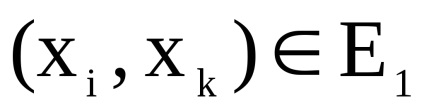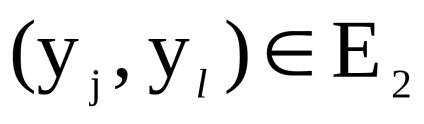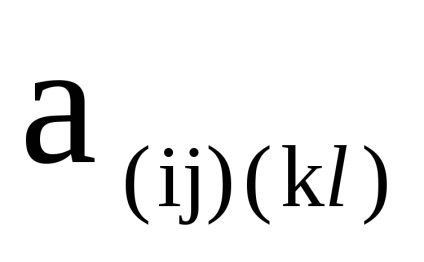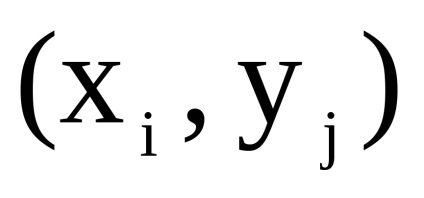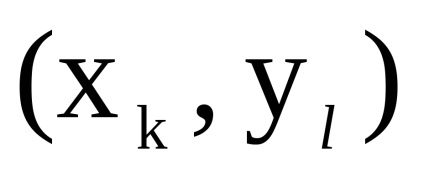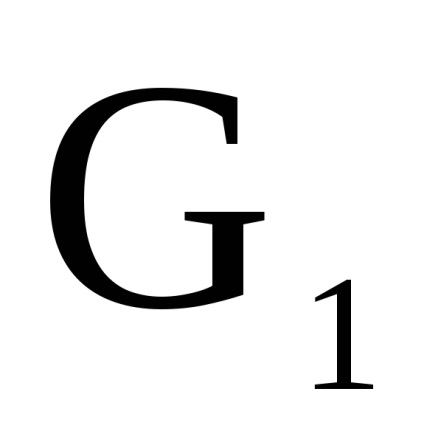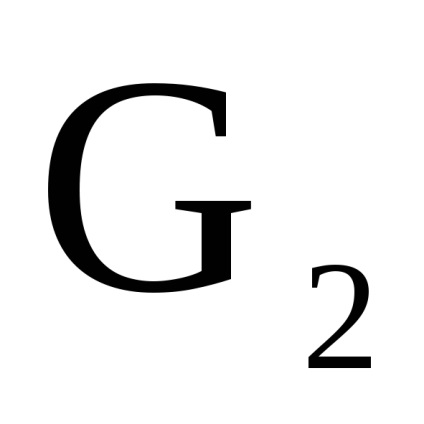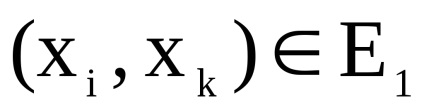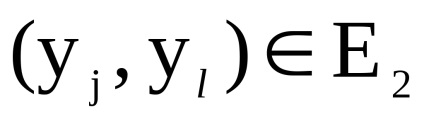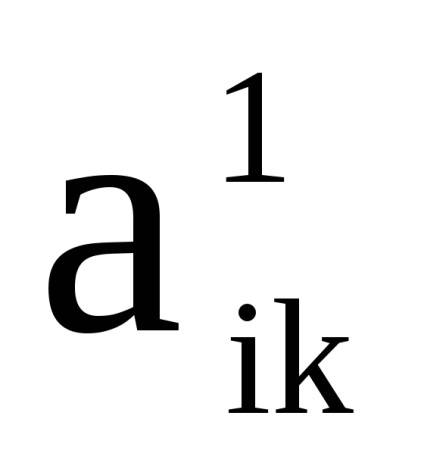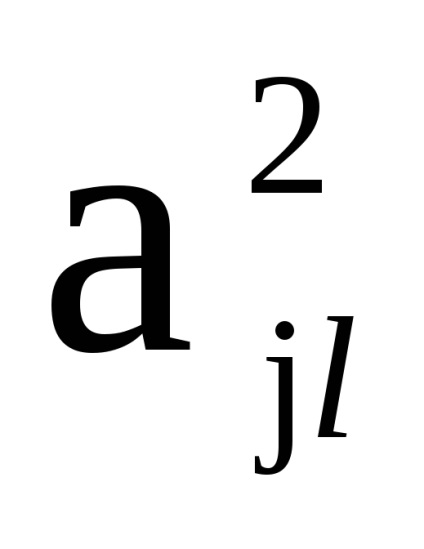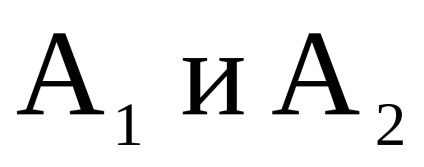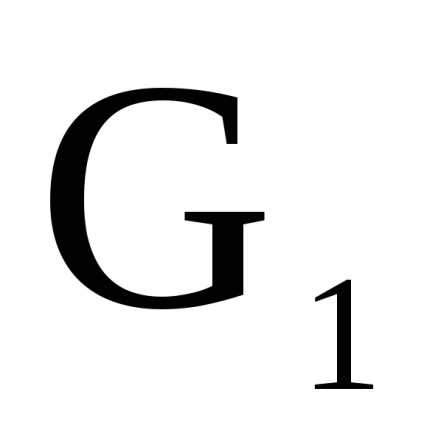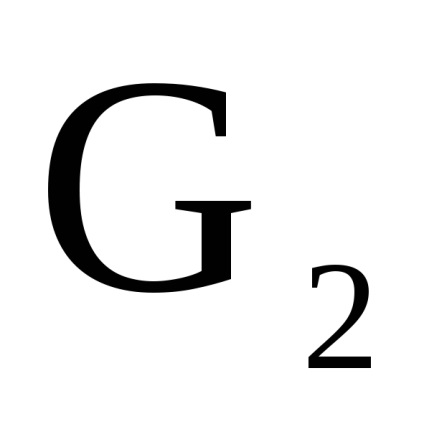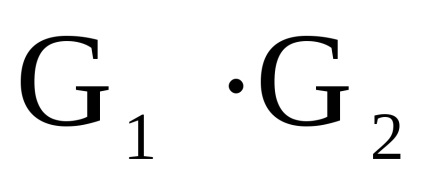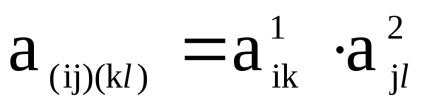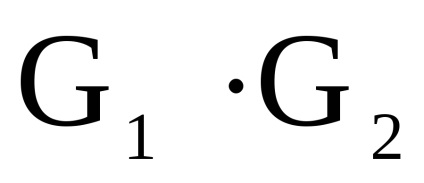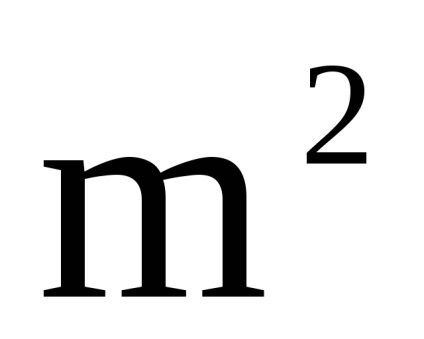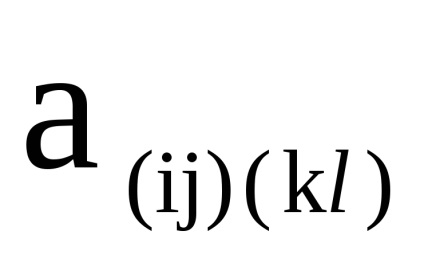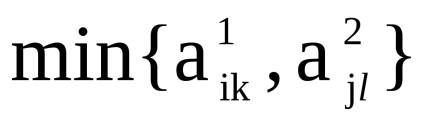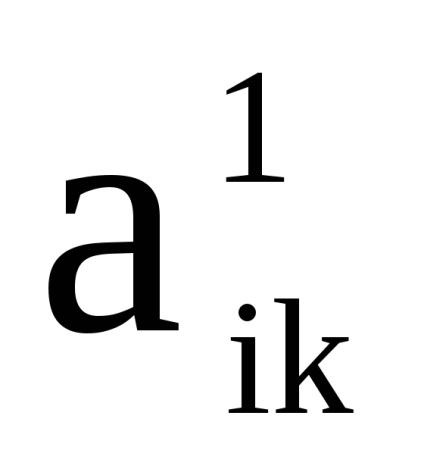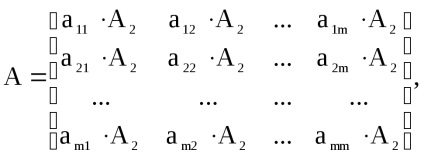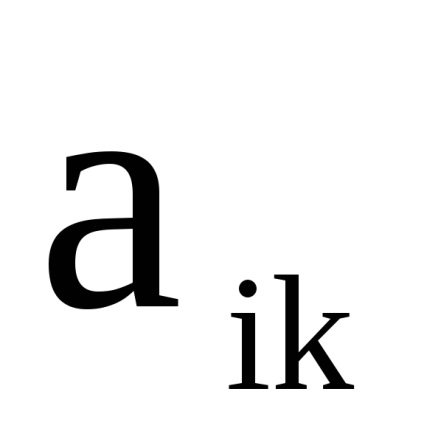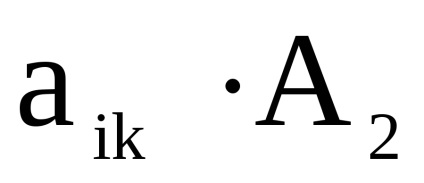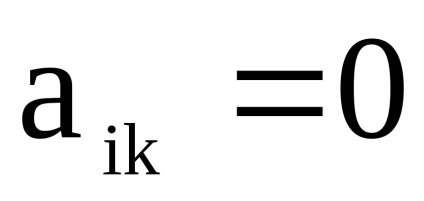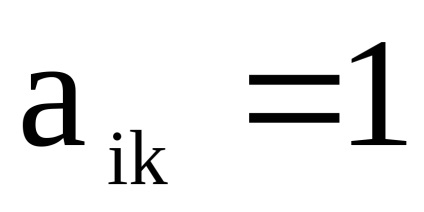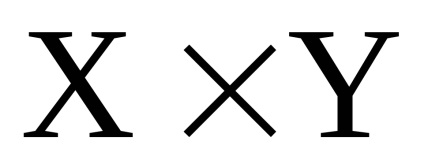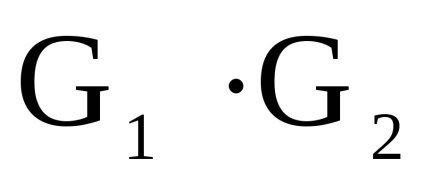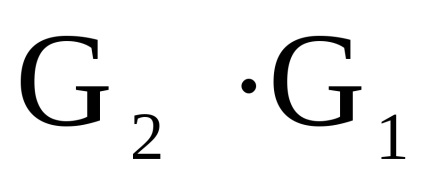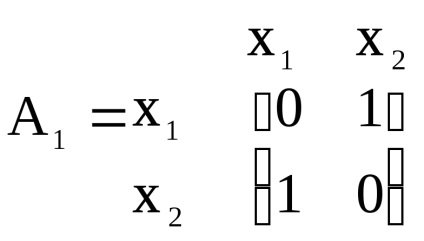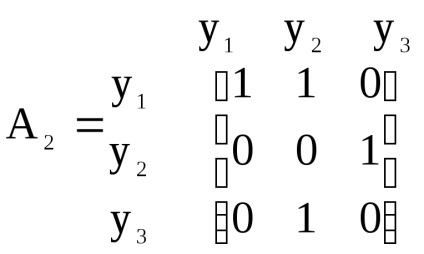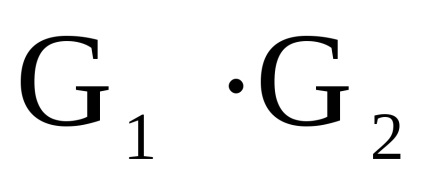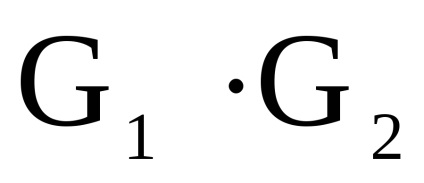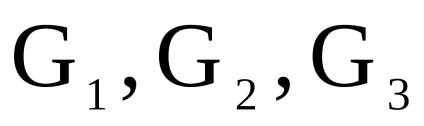lăsa
și - două grafice orientate simultan sau nedirecționate cu seturi disjuncte de vârfuri. Un produs directNumără Graficul cu un set de vârfuri în care arcul (marginea) de la vârf la început există dacă și numai dacă există arce (marginile) și în același timp.Să luăm în considerare funcționarea produsului direct al grafurilor în formă de matrice.
Teorema 2.2.6. lăsa
și - două grafice orientate simultan sau nedirecționate cu seturi disjuncte de vârfuri, Sunt matricele vârfurilor lor, respectiv. Apoi, matricea de adjacitate a vârfurilor graficului este o matrice de dimensiuni în care elementul , indicând numărul de arce (marginile) care conectează vârful cu , se calculează după cum urmează:
,
unde
și - elemente de matrice respectiv, , .
Dimensiunea matricei este egală, a. Prin definiție, în grafic există un arc (o margine) care vine de la vârf la început , dacă și numai dacă există arce simultan (muchii) și . Elementul matricei de adjunct A a graficului G determină numărul de arce (marginile) de la vârf la început . Găsirea numărului de arce (marginile) graficelor și , pentru care și , corespunde operațiunii de a lua minimum de elemente și matrici respectiv.
Corolar. Dacă graficele
și nu au mai multe arce (marginile) și o buclă într-un grafic nedirecționat nu este considerată dublă, atunci când se calculează elementele matricei de adjuvantitate a vârfurilor graficului operația de a lua elementul minim corespunde calculului produsului obișnuit sau logic:
.
Notă. Pentru a simplifica și accelera procesul de calcul al elementelor matricei de adjuvantitate a vârfurilor graficului
utilizăm următoarea observație. Fără pierderea generalității, presupunem asta. Ordonăm coloanele și rândurile matricei A în modul următor: Apoi, matricea poate fi împărțită în blocuri care corespund elementelor matricei A1. dimensionalitatii . Element al fiecărui bloc a stabilit i și k vor fi calculate ca , în plus Este un element fix al matricei A1. Dacă elementele matricelor A1 și A2 iau doar valorile 0 și 1, atunci produsul direct (tensor) al matricelor:
unde
scalar înmulțit cu matricea A2. este egal cu 0 dacă , și este egal cu A2. dacă .
Primer2.2.6. Funcționarea produsului direct al graficelor este prezentată în Fig. 2.2.12.
Este evident că corespondența dintre elementele seturilor
și definește un izomorfism al grafurilor și , ceea ce este valabil și în cazul general.
Formăm matricele contiguității vârfurilor graficelor originale și.
, .
Conform corolarului Teoremei 2.2.6 și a remarcii, matricea de adjuvantitate a vârfurilor graficului
are forma:
Nu este greu de verificat dacă matricea de adjuvantitate a vârfurilor A corespunde graficului
, prezentat în Fig. 2.2.12.
Funcționarea unui produs direct al grafurilor are următoarele proprietăți care rezultă din definiție, precum și proprietățile produsului cartezian al seturilor și sunt valabile pentru orice grafice orientate simultan sau nedirecționate
cu seturi disjuncte de vârfuri:
Funcționarea unui produs direct poate fi extinsă prin inducție la orice set finit de grafice orientate sau nedirecționate cu perechi de seturi disjuncte de vârfuri:
.
Articole similare