Din definiția factorului de integrare pe care îl avem
sau, împărțind ambele părți ale (10.20) prin,
Avem în forma (10.20) și (10.20 „), o ecuație diferențială parțială pentru funcția necunoscută. Problema integrării acestei ecuații nu, în general, mai ușor decât problema rezolvării ecuației (10.6). Desigur, trebuie să cunoaștem doar o singură soluție particulară a ecuației (10.20), uneori pe unele caracteristici ale ecuației (10.20), se poate găsi o soluție specială, și apoi integrarea ecuației (10.6) se reduce la cvadratură.
Luați în considerare, de exemplu, cazul în care există un factor de integrare care este o funcție de x singur.
În acest caz, = 0 și ecuația (10.20 ') devine
Este clar că existența unui factor de integrare, nu dependent este necesar și suficient ca partea din dreapta să fie o funcție de x, atunci există Zona:
Exemplul 10.6: (2yx + x2y +) dx + (x2 + y2) dy = 0
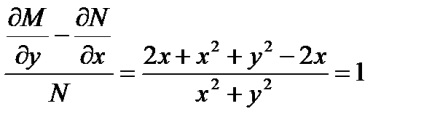
Prin urmare, = 1, = x, = e x
există o ecuație în totalul diferențelor. Noi o integrăm,
Pentru a găsi (y), noi calculam și echivalăm N
și integrala generală a ecuației noastre este
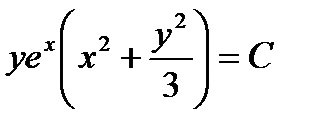
Considerăm cazul particular al unui factor de integrare care depinde doar de x, atunci când N = 1, în acest caz ecuația are forma
Ecuația (10.21) are forma
cu condiția. aceasta este o funcție a unui x.
În acest caz, f (x, y) are forma
și anume o ecuație scrisă în forma (10.22) și admiterea unui factor de integrare care depinde numai de x este o ecuație liniară.
Din ecuația (10.21) avem
Privind notația cursului 9 pentru o ecuație liniară, ajungem la concluzie.
Ecuația liniară are un factor de integrare
Exemplul 10.7: Ecuația are o integrare
factor. înmulțind ambele părți ale ecuației prin ea, avem
unde partea stângă este diferența totală, integrând