Termenul "proces stocastic" se referă la câmpul haosului, la comportamentul dezordonat, la un proces a cărui dinamică este aleatoare și imprevizibilă. Un exemplu binecunoscut al unui astfel de proces este mișcarea Browniană.
Cuvântul "rezonanță" în cel mai general sens înseamnă un răspuns puternic al unui sistem la un mic efect extern. Ceea ce este important este că un astfel de răspuns puternic este selectiv, adică se produce numai sub anumiți parametri ai influenței externe. Rezonanța apare dacă frecvența acțiunii externe este comparată cu frecvența de oscilație naturală a sistemului.
Împreună, aceste două cuvinte reprezintă un foarte interesant și, la prima vedere, contradictoriu fenomen de bun simț, care apare în multe, complet diferite sisteme și chiar, după cum se dovedește, a fost folosit de mult de natură.
Acest fenomen a fost descoperit în anii 80. Esența rezonanței stochastice este că adăugarea la sistemul de zgomot, adică haosul haotic, nu reduce, ci intensifică răspunsul sistemului la un impact periodic slab. În același timp, zgomotul nu numai că nu suprimă semnalul, ci, dimpotrivă, îi ajută să se manifeste. Cel mai puternic efect apare la o anumită intensitate optimă a zgomotului.
Oricine a întâmpinat problema izolării unui semnal util de zgomot, pare evident că primul pas în acest proces este reducerea maximă posibilă a intensității zgomotului. Încă de la începutul ingineriei radio, când inginerii au auzit pentru prima oară sunetul de la difuzoare, ei caută modalități de a suprima zgomotul care apare în mod inevitabil în circuitele electrice și în sistemele de comunicații. Se crede că generarea zgomotului este necesară numai în situațiile în care este necesar să nu se dea cineva încredere pentru a lua un semnal util.
Ideea de a folosi zgomot pentru a îmbunătăți calitatea semnalului pare absurd, pentru că orice persoană normală ar gândi, de exemplu, zgârierea un CD, pentru a citi informația a devenit mai bine de la ea. Cu toate acestea, studii recente sugerează că, în anumite cazuri, zgomotul poate juca un rol constructiv în percepția semnalelor slabe datorită efectului numit "rezonanță stocastică". Fenomenul a fost atât de neobișnuit încât prima dată după deschidere, a atras atenția unui număr foarte limitat de oameni de știință, în special cei care l-au și găsit.
Rezonanța stocastică este amplificarea unui semnal periodic sub influența zgomotului alb al unei anumite puteri. Este un fenomen universal inerent în multe sisteme neliniare care se află sub influența externă a efectelor periodice haotice și slabe.
Pentru a explica acest fenomen, considerăm un sistem bistabil care are disipare și frecare. Sub influența suficientei influențe externe, un astfel de sistem se poate transforma într-o altă stare. Dacă influența externă suficientă este periodică, atunci sistemul va trece de la o stare la alta. Un efect insuficient (subthreshold) nu va cauza un răspuns de la un astfel de sistem. Dacă impactul exterior este aleatoriu (zgomot), atunci sistemul "se rătăcește" aleatoriu și, după un timp nedefinit, lungimea medie a acestuia depinzând de puterea de zgomot, poate să sară dintr-o poziție în alta. Dinamica acestor saltări va fi neregulată.
Să analizăm acum efectul total al efectelor sub-prag periodice și haotice. În sine, o perturbație periodică subthreshold nu va putea să transfere sistemul într-o altă stare, dar zgomotul îl ajută prin aducerea unui impact asupra stării "critice". Ca urmare, răspunsul sistemului manifestă o periodicitate determinată de un impact periodic slab.
Raportul optim (care conduce la raportul maxim dintre semnal și zgomot) este puterea de zgomot la care durata de viață caracteristică a sistemului într-o stare este egală cu jumătate din perioada perturbării periodice. Prea mult sau prea puțin zgomot conduce la un sistem mai puțin sensibil la un impact periodic slab.
Condiția pentru apariția rezonanței stohastice - sistemul trebuie să fie non-linear, sau de răspuns al sistemului la efectul net va fi pur și simplu suma răspunsurilor și nu va duce la orice efecte noi.
Sistemul trebuie să aibă cel puțin două stări stabile sau metastabile. Acest lucru poate fi fie un sistem bistabil, fie un sistem cu o stare excitată de lungă durată metastabilă.
Sistemele care demonstrează rezonanța stocastică includ, de exemplu: dinamica perioadelor glaciare de pe Pământ; dinamica climatului nord-atlantic; pompare într-un laser cu inel; organe senzoriale într-un număr de animale.
Luați în considerare, de exemplu, un sistem bistabil. Cuvântul "sistem bistabil" este un sistem cu două poziții de echilibru stabil. Un exemplu mecanic simplu este mișcarea unui punct material într-un potențial cu două minime (vezi figura 1a). În cazul în care particula este acționat încă și forța de frecare, este clar că, indiferent de ce am ales condițiile inițiale, fluctuații în cele din urmă, mor, particula „căderea“ într-una dintre potențialele puțuri, și va rămâne acolo pe termen nelimitat.
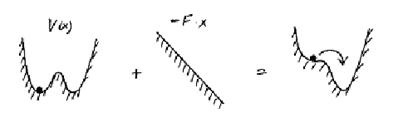
Fig. 14.6 Exemplu de comportament al unui sistem bistabil cu influență externă asupra acestuia.
Pentru ca particula să cadă într-o altă groapă potențială, este necesară exercitarea unei forțe externe. Dacă această forță este suficient de mare, ea va "trage" particula din prima groapă și o va arunca în a doua. În limba potențială (în acest text, potențialul este folosit ca sinonim pentru energia potențială), "aplicarea unei forțe externe" înseamnă adăugarea unui potențial de creștere liniară, așa cum se arată în Fig. 14b. Dacă V (x) este un potențial bistabil, atunci forța externă ar trebui să depășească valoarea = | V '(x) |, luată la punctul de inflexiune, adică unde forța de refacere creată de potențial este cea mai mare. Apoi, potențialul total se modifică după cum se arată în figură, iar particula se alunecă în al doilea godeu. Dacă forța externă este periodică în timp, atunci particula va "sări" de la un fântână la altul și înapoi. Ca rezultat, sistemul bistabil va răspunde la un impact extern puternic. În acest caz, frecvența cu care sistemul sare de la o stare stabilă la alta coincide cu frecvența acțiunii externe. Dacă impactul exterior este foarte puternic, atunci sistemul va repeta în mod ascultător toate schimbările și fluctuațiile acestei forțe. Dacă impactul exterior nu este atât de puternic, adică <, то частица не сможет покинуть яму и останется в ней, несмотря на внешнее воздействие.
Astfel, un sistem bistabil poate avea un anumit prag de sensibilitate: pentru o forță exterioară, sistemul începe să sară dintr-o stare în alta cu o frecvență a forței exterioare și când <система не чувствует внешнее воздействие. То есть, у бистабильной системы существует некий порог чувствительности к внешним воздействиям. Слишком слабые, т.е. подпороговые воздействия остаются для системы незамеченными, но при дополнительном воздействии на такую систему, даже стохастическим сигналом может происходить усиление сверхслабых сигналов.
Fig. 14.7 Semnalele a) și imaginile lor Fourier b).
Semnalul stochastic are un zgomot aleator. Cu ajutorul transformării Fourier este posibilă separarea semnalului periodic de zgomot.
În sistemul bistabil luat în considerare, o forță aleatorie va produce oscilații aleatorii. S-ar putea să se întâmple ca o particulă, rătăcind în jurul valorii de un potențial bine, să sară dintr-o dată la a doua. Evident, cu cât zgomotul este mai puternic, cu atât este mai scurt timpul de salt, adică cu atât mai des particulele sare de la o groapă la alta. Dacă prezentăm dependența coordonatelor particulelor la timp, obținem aproximativ aceeași imagine ca în Fig. 14.8.
Fig. 14.8 Răspunsul sistemului la un impact extern accidental.
Dacă un zgomot extern și un add slab semnal periodic subthreshold, atunci particula va continua să sări de la un bine la altul, dar natura acestui proces se schimbă: componenta periodică apare în aceasta, cu o perioadă egală cu perioada semnalului extern este slab. Adică, sarele apar datorită forței aleatorii, iar aditivul periodic "modulează" efectul (adică își adaugă periodicitatea proprie).
Zgomotul, așa cum este, elimină o barieră potențială de neegalat și determină sistemul să răspundă la semnalul sub-prag.
Aceasta este esența rezonanței stochastice (amplificare). Particularitatea rezonanței stochastice constă în faptul că există o intensitate optimă a zgomotului la care răspunsul sistemului la semnalul periodic este cel mai puternic. Pentru a determina cât de mare este acest răspuns, este necesar să construim dependența coordonatelor particulelor în timp și folosind transformarea Fourier pentru a izola componenta periodică a semnalului. Apoi, amplitudinea "cocoșului" adițional al transformării Fourier (Figura 14.7) va servi ca o caracteristică cantitativă a sensibilității sistemului. Cu cât este mai mare cocoașă, cu atât mai puternic apare semnalul periodic extern în mișcarea particulei.
Fig. 14.9 Răspunsul unui sistem bistabil la diferite intensități ale zgomotului.
Figura arată dependența coordonatelor particulelor în timp pentru același semnal periodic slab, dar pentru intensități diferite ale zgomotului. Se observă că atunci când intensitatea zgomotului este mică, particula se află într-o fantă potențială pentru o lungă perioadă de timp înainte de a sări la alta (vezi figura 14.9, graficul de jos). Un semnal periodic extern nu apare aici. La creșterea intensității zgomotului la un agregat optim de particule sub influența zgomotului și o forță periodică va sări de la un sincronă bine la cealaltă (fig. 14.9, panoul din mijloc). Componenta periodică a răspunsului sistemului este clar vizibilă, perioada în care coincide cu perioada forței externe. În cele din urmă, cu amplificarea ulterioară a zgomotului, mișcarea particulei devine din ce în ce mai haotică; Componenta periodică a răspunsului va scădea (Figura 14.9, graficul superior).
O dependență tipică a răspunsului sistemului la intensitatea zgomotului extern este prezentată în Fig. 14.10. Se poate observa că pentru o anumită intensitate a zgomotului, răspunsul sistemului la semnalul util va fi maxim.
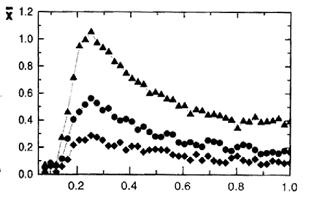
Fig. 14.10 Dependența de intensitatea zgomotului din amplitudinea semnalelor componentei periodice.
O intensitate definită a zgomotului corespunde unui timp mediu foarte specific de alunecare de la un fântână la altul. Condiția pentru intensitatea optimă a zgomotului: este necesar ca timpul de propagare cauzat de acest zgomot să fie egal cu jumătate din perioada unei perturbații periodice slabe. Când sincronizarea perioadei de hop și a perioadei de forță externă are loc, se produce cel mai puternic răspuns al sistemului la o perturbare periodică externă (rezonanță). Dacă aceste două procese nu sunt sincronizate, sensibilitatea la forța periodică slabă scade.
Rezonanța stocastică este utilizată în tehnologie, observată în funcționarea organismelor vii. De exemplu, rezonanța stochastică este utilizată în sistemele optice și apare când se generează impulsuri nervoase.
Un exemplu de sistem optic în care a fost observată rezonanța stocastică este așa numitul laser inelar (Fig.), În care lumina laser este pompată într-un rezonator cu trei sau mai multe oglinzi. În acest sistem, există două moduri stabile de pompare a luminii laser atunci când lumina se mișcă în direcția mișcării în sensul acelor de ceasornic sau în sens contrar acelor de ceasornic. Acesta a fost unul dintre primele experimente (1988), când a fost observată rezonanța stochastică în laborator.
La începutul anilor 90, sa realizat ca rezonanta stocastice poate juca un rol-cheie în procesele neurofiziologice, și anume funcționarea rețelelor neuronale în transmiterea impulsurilor de la un neuron la un alt grup.
Destul de recent, în a doua jumătate a anilor 1990, a apărut problema posibilității existenței unei rezonanțe stocastice la nivelul cuantic. Este de așteptat ca "cufundarea particulelor" cuantice, care există întotdeauna, chiar și la temperatura zero absolută și care joacă aici rolul de zgomot, va facilita detectarea unui semnal cuantic, diseminarea informațiilor etc.
Rezonanța stocastică poate apărea și în alte sisteme decât rezonanțele bistabile. Principala cerință este prezența unui prag. Un exemplu al unui astfel de sistem este un sistem în care nu se produce o alunecare între două poziții stabile de echilibru, ci între stările "de bază" și "excitate" ale sistemului.
Recent, a fost descris un fenomen numit "rezonanță dublă stocastică". Aici două tipuri de zgomot acționează simultan asupra particulei libere: prima creează ceva asemănător unui potențial bistabil, iar al doilea forțează particula să sară în acest pseudopotențial. Fenomenul este foarte interesant, deoarece servește ca o ilustrare excelentă a faptului că zgomotul nu numai că poate distruge procese subtile, corelate, ci, dimpotrivă, le dă viață.
Este interesant că în viitorul apropiat, când electronica subminiată va părăsi laboratoarele științifice și va deveni disponibilă pentru utilizatorul de masă, rezonanța stocastică se poate dovedi a fi o parte importantă a acesteia.
Un alt exemplu îl reprezintă rețelele neuronale - dispozitive electronice capabile să proceseze eficient cantități uriașe de informații. În astfel de rețele, rezonanța stocastică se va manifesta sub forma unei conductivități îmbunătățite a informațiilor zgomotoase și a sincronizării proceselor care apar simultan în diferite părți ale rețelei.
În ultimii ani, au apărut o serie de rapoarte privind utilizarea cu succes a rezonanței stochastice în procesarea semnalelor și recunoașterea imaginilor pe computer.
Înapoi la Cuprins: Cercetări fundamentale și aplicate moderne în domeniul instrumentelor