Informații teoretice despre paralelismul dreptunghiular: pentru munca unui tutore de matematică cu elevii de liceu și pregătirea pentru USE.
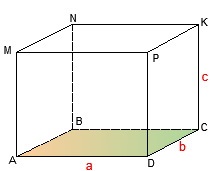
Proprietățile unui paralelipiped dreptunghiular cu lungimea a, lățimea b și înălțimea c:
1) Toate fețele sale sunt dreptunghiulare. Feretele opuse sunt dreptunghiuri egale.
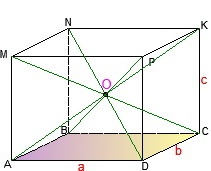
3) Punctul de intersecție al diagonalelor este centrul sferei descrise
4) Pătratul diagonalei AK a unui paralelipiped dreptunghiular (vezi figura) este egal cu rădăcina pătrată a sumei pătratelor lungimilor dimensiunilor sale, adică,
Dovada. Luați în considerare triunghiul drept AKC. Potrivit teofaniei lui Pitagora (a se vedea figura precedentă). Acum, în triunghiul ADC :. Rămâne să inserați prima egalitate în locul laturii drepte a ultimei.
5) Volumul oricărui paralelipiped dreptunghiular este egal cu produsul lungimilor dimensiunilor sale, adică,
6) Suprafața de suprafață S = 2ab + 2bc + 2ac
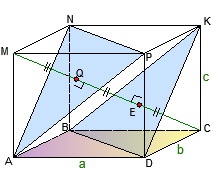
8) Proprietatea diagonalelor cubului: diagonala MC ABCDMNKP- perpendicular pe planuri (ANP) și (KBD)
- împarte aceste planuri în trei segmente egale: MQ = QE = EC
Piggy bancă sarcini de tutore în matematică pe un parallelepar
1) laturile bazei într-un paralelipiped dreptunghiular sunt egale și 4 cm. Diagonala are un unghi cu o margine laterala mai mica. Găsiți înălțimea paralelipipedului.
2) Diagonala într-un paralelipiped dreptunghiular este egală cu și formează unghiuri și cu două fețe laterale adiacente. Determinați volumul acestei casete.
3) În cub ,. Găsiți MN dacă marginea cubului este egală cu.
Notă a tutorelui de matematică: Dacă există numere incomode pentru calcule, cum ar fi sfaturile profesorilor de matematică să recurgă la similitudine. Pentru a rezolva problema pentru unele de dimensiuni convenabile coaste, de exemplu, de 2 cm, și apoi înmulțit cu răspunsul primit
4) În cub ,. Găsiți MN dacă marginea cubului este egală cu
5) Într-un paralelipiped dreptunghiular ABCDEFGH AB = 6cm, BC = 8cm. Prin mijlocul laturilor AD și CD și vârful F planul este desenat, la un unghi față de planul bazei. Găsiți suprafața completă a cutiei.
6) În paralelipiped dreptunghiular ABCDTKLP: AB = 3cm, BC = 4cm. Un plan este tras prin diagonala KD a acestei paralelipiped paralele cu diagonala AC. Determinați unghiul format de acest plan și planul bazei, dacă volumul cuboidului.
7) Într-un paralelipiped dreptunghiular ABCDSQPE: AB = 6m, AD = 3m, AS = 4m. Prin punctele M, N și K, marginile laterale ale paralelipipedului sunt împărțite astfel încât AM: MB = 1: 1, SN: NQ = 5: 1, EK: KP = 1: 2. Calculați suprafața secțiunii prin planul MNK.
8) Într-un paralelipiped dreptunghiular, ABCDFESQ: AB = 3m, AD = 10m, AF = 4m. Punctele M, N și K își împart marginile laterale în segmente astfel încât AM: MD = 1: 4, FN: NQ = 2: 3, EK: KS = 1: 2. Calculați suprafața secțiunii formată de planul MNK.
Alexander Nikolayevich Kolpakov,
tutor în matematică la Moscova. Lecții private în Strogino
Desigur, bine făcut. Și ce știi despre planurile optime în probleme de programare liniară?
Nu sunt un tutore pentru programarea liniară, deși am o idee atât despre metoda simplex cât și despre sarcina de transport. Profilul meu este matematica clasică, matematica școlară, pregătirea pentru EGE și GIA. Deși anul trecut a ajutat studenții săi, care au intrat în Academia Financiară cu programare liniară. Dar nu te îngropa în ea ...