Subiect: Elemente ale teoriei funcțiilor trigonometrice
Lecție: cerc numeric
1. Tema lecției, introducere
Scopul nostru imediat este definirea funcțiilor trigonometrice: sinus. cosinus. tangentă. kotangens-
2. Cerc numeric
Un argument numeric poate fi amânat pe o linie de coordonate sau pe un cerc.
Un astfel de cerc este numit numeric sau unitar, deoarece pentru comoditate luăm un cerc cu
De exemplu, un punct este dat. Marcați-l pe linia de coordonate
și pe un cerc numeric.
Când lucrați cu un cerc numeric, sa convenit că mișcarea în sens invers acelor de ceasornic este pozitivă, în sensul acelor de ceasornic - negativ.
Sarcinile tipice - trebuie să stabiliți coordonatele unui anumit punct sau, invers, să găsiți un punct din coordonatele sale.
Linia de coordonate stabilește o corespondență unu-la-unu între puncte și numere. De exemplu, numărul corespunde punctului A cu coordonatele
Fiecare punct B cu o coordonată este caracterizat de un singur număr - o distanță de la 0 la cea luată cu un semn plus sau minus.
Pe un cerc numeric, o corespondență unu-la-unu funcționează numai într-o singură direcție.
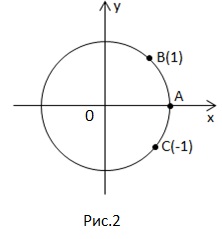
De exemplu, există un punct B pe cercul de coordonate (figura 2), lungimea arcului fiind 1, adică, acest punct corespunde cu 1.
Se dă un cerc, lungimea unui cerc Dacă este atunci lungimea cercului unității.
Dacă adăugăm, vom obține același punct B, dar - de asemenea, se încadrează în T B, scade -. La fel B ..
Luați în considerare punctul B: lungimea arcului = 1, atunci numerele caracterizează m. B pe un cerc numeric.
Astfel, numărul 1 corespunde unui singur punct al cercului numeric - punctul B, iar punctul B corespunde unui număr infinit de puncte ale formularului.
Pentru un cerc numeric următoarele sunt adevărate:
Dacă un număr de cerc din numărul unui număr corespunde unui număr, atunci acesta corespunde unui număr din formular
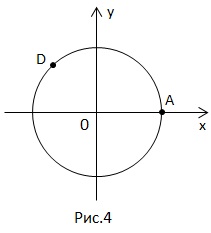
Puteți face orice număr de revoluții complete în jurul cercului numeric în direcția pozitivă sau negativă - punctul este același. Prin urmare, ecuațiile trigonometrice au un număr infinit de soluții.
De exemplu, punctul dat este D. Care sunt numerele la care corespunde?
setul de numere care corespund punctului D.
3. Punctele de bază ale unui cerc
Să luăm în considerare punctele de bază pe un cerc numeric.
lungimea întregului cerc.
.
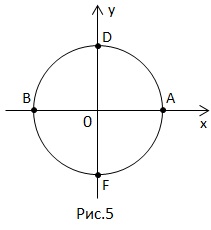
Adică, înregistrarea setului de coordonate poate fi diferită.
4. Exemple
Să luăm în considerare sarcinile tipice pe un cerc numeric.
1. Având în vedere :. Găsiți: un punct pe un cerc numeric.
Am alocat întreaga parte:
.
Este necesar să găsiți m într-un cerc numeric. , atunci.
În acest set include un punct.
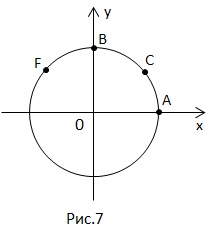
2. Este dat :. Găsiți: un punct pe un cerc numeric.
Este necesar să găsiți m.
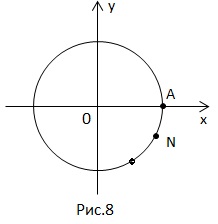
așa se face acest lucru.
Rezolvarea problemei de corespondență standard, între numere și puncte de pe circumferința numerică, am constatat că este posibil ca fiecare număr să găsească un singur punct și pot fi găsite pentru fiecare punct al setului de numere care sunt caracterizate prin acest punct.
Împărțim arcul în trei părți egale și marchează punctele M și N.
Să găsim toate coordonatele acestor puncte.
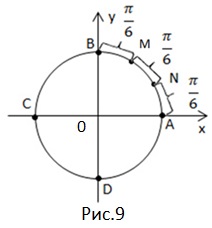
5. Concluzie
Deci, scopul nostru este de a defini funcțiile trigonometrice. Pentru a face acest lucru, trebuie să învățăm cum să specificăm argumentul funcției. Am considerat punctul de cercul unitate, și a rezolvat două sarcini comune - pentru a găsi un punct de pe cercul real, și scrie toate coordonatele punctului de cercul unitate.
Lista recomandărilor recomandate
Linkuri recomandate pentru resursele de internet
1. Deschide matematica.
Recomandări tematice
Nr. 531; 536; 537; 541; 552.
Se încarcă.
Se încarcă.
Lucrări populare
- Peisaje în versurile lui Alexander Puskin
- O analiză a poeziei de către A. Blok "Pe câmpul Kulikovo"
- Tată și fiu în povestea lui D. Aldridge "The Last Inch"
- Viața și munca Goethe V. Și
- Deciziile instanței de arbitraj. sarcini
- Proiectarea unei întreprinderi de catering public Proiectarea unui snack bar. partea 2
- A. S. Pushkin și S.A. Yesenin despre natura rusă
-
Statistici privind proiectele
Articole similare