Toate produsele pot fi împărțite în nereparate și reparate. Performanța produselor nereparate după eșecul lor nu este restabilită. Acest lucru se datorează caracteristicilor lor fizico-chimice sau structurale și, uneori, considerentelor economice. Aceste produse pot fi supuse unei întrețineri preventive.
Timpul de funcționare de la începutul funcționării produsului neasamblat la defectarea sa se numește timpul de funcționare defectuos sau timpul de funcționare fără probleme. MTBF este o variabilă aleatorie continuă. Restaurarea operabilității produsului reparate după o defecțiune este asigurată de proiectant atunci când proiectează acest produs.
Adesea, produsele constau dintr-un număr mare de elemente, fiecare dintre ele rareori eșuează. Probabilitatea apariției simultane a două eșecuri în astfel de produse este zero, iar fluxul de defecțiuni este denumit obișnuit. Dacă probabilitatea apariției defecțiunilor într-un anumit interval de timp nu este afectată de prezența lor la nici un interval anterior, un astfel de flux de defecțiuni este numit fir fără consecințe.
În perioada inițială de funcționare a produselor complexe (în timpul pauzei) numărul mediu de eșecuri pe unitatea de timp nu este constantă, iar fluxul de eșecuri se numește nestaționare. La finalul perioadei de încălzire numărul mediu de eșecuri pe unitatea de timp devine constantă.
- Calculați timpul mediu de funcționare până la defecțiunea T a injectorilor luați în considerare. Inițial, calculele se fac direct din valorile eșantionului T și apoi se utilizează o serie statistică.
Pentru a calcula valoarea medie a T a unei variabile aleatoare T direct de la valorile sale de eșantion t1. TI. tN utilizați formula:
Calculele care utilizează seria statistică:
Intreaga gama de valori observate T divizate în intervale de m sau „biți“ și numărul de valori conta ni. pentru fiecare cifră i-a și scrieți toate datele din tabel.
Tabelul 1. Conversia timpului de funcționare la eșecul seriei statistice.
Probabilitatea statistică qi a unei variabile aleatorii care intră în intervalul i se calculează astfel:
Reprezentăm grafic seria statistică obținută:
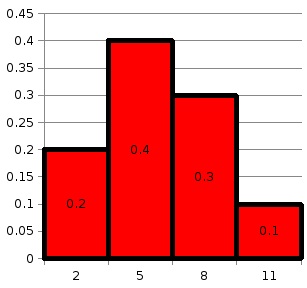
Fig. 1 Seria statistică a timpului de funcționare până la eșec.
Pentru a calcula valoarea medie a unei variabile aleatorii ca "reprezentant" al tuturor valorilor sale care aparțin intervalului i, luați-i mijlocul. Atunci timpul mediu până la defect este definit ca (4)
Calculul folosind formula (4) introduce unele erori metodologice. Cu toate acestea, valoarea sa este de obicei neglijabilă. Această eroare poate fi estimată prin formula:
Unde sunt valorile medii.
Concluzie: în această alocare, timpul mediu de eșec a fost calculat din valorile eșantionului T și utilizând seriile statistice. Timpul mediu de funcționare pentru proba T = 5,84 * 10 3 h diferă puțin față de valoarea folosind seria statistică 5,96 * 10 3 h.