În cele din urmă, lasă două tangente reciproce perpendiculare t1 și t2 să fie extrase din punctul P către elipsă (vezi Figura 17).

Reflectati linia focus relativ la t2, iar punctele sunt conectate la F. Evident, unghiul - linia (acesta din urmă rezultă din faptul că unghiul dintre t1 și t2 linia și oa doua teorema Poncelet); Prin urmare. dar; prin urmare,. Pe de altă parte, PO este mediana unui triunghi, deci. Având în vedere ecuația anterioară obținem: PO 2 = 2a 2 - c 2 sau PO 2 = (2 - c 2) + a 2 = a 2 + b 2. adică nodurile unghiuri drepte, ale căror laturi sunt tangente la elipsei sunt situate pe un cerc .. rază cu centrul în centrul elipsei.
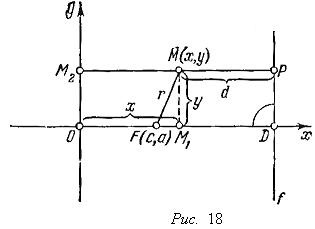
Elipsa ca urmare a comprimării cercului. Lăsați punctul M. care aparține elipsei să fie îndepărtat de la axa principală x prin distanța MM1 = y. și din axa principală y - până la distanța MM2 = x (a se vedea figura 18). Simetria permite elipsă restricționați elipsă considerare la puncte situate în interiorul unuia dintre unghiurile formate de axele x și y principal. Din relațiile (2) rezultă:
După excluderea r și d. obținem:
de unde, înmulțind ambele părți ale egalității cu și luând în considerare relațiile (2). găsim în cele din urmă:
Elipsa ca urmare a comprimării cercului.