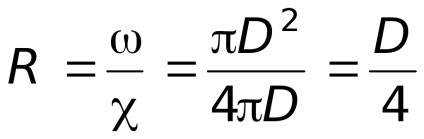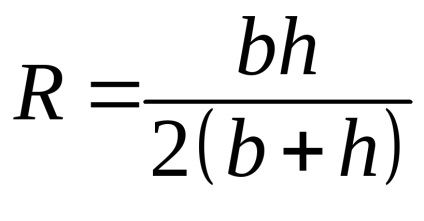Pe baza ecuației Bernoulli, au fost proiectate o serie de instrumente, cum ar fi un venturi, o pompă cu jet de apă, un ejector, carburatoare cu motoare cu piston,
Exemplul 1. Venturiul este un tub scurt, tăiat în afară, cu o îngustare în mijloc (Figura 3.13). În partea largă și în munți sunt instalate fie piezometre, fie un indicator de presiune diferențială.
Aplicăm ecuația Bernoulli pentru secțiunile 1-1 și 2-2 fără a lua în considerare pierderile și
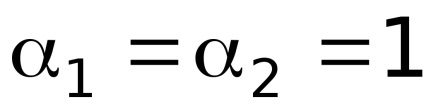

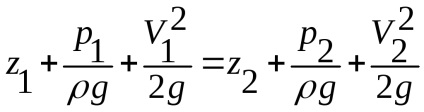
Transformăm ecuația după cum urmează:

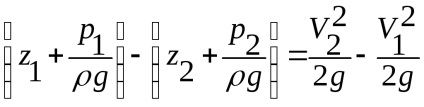
În conformitate cu (Figura 3.13), diferența din partea stângă este h.
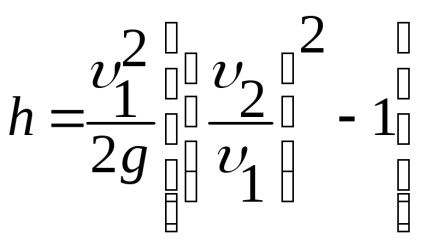
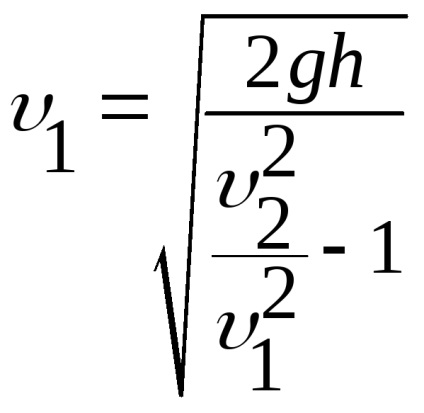
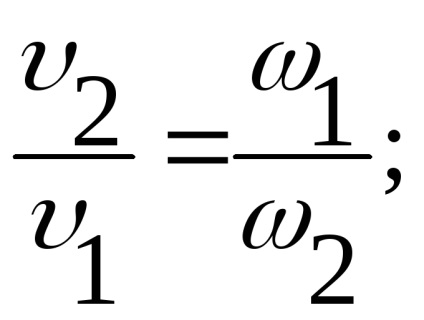
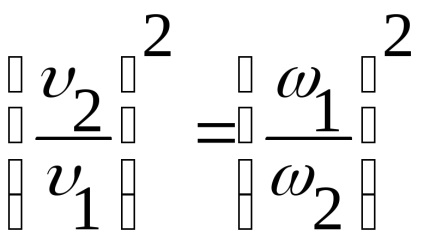

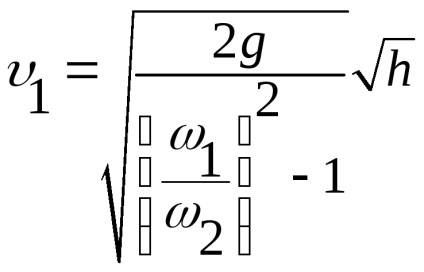
Utilizând ecuația fluxului
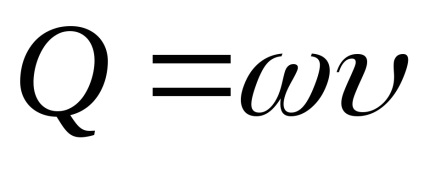
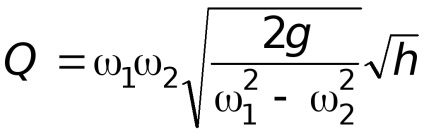
Indicăm constantele prin
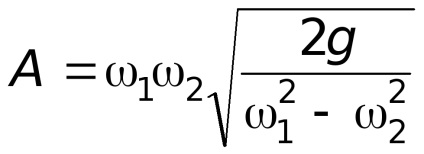
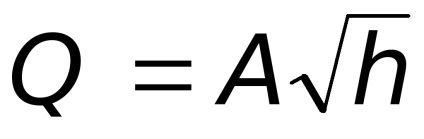
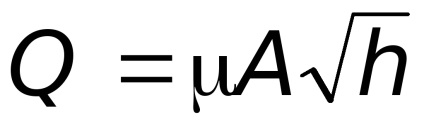
coeficientul de descărcare a contorului de apă.
Exemplul 2. Carburatorul motoarelor cu ardere internă cu piston servește la alimentarea benzinei și amestecarea acesteia cu debitul de aer (Figura 3.14). Fluxul de aer, aspirat în motor, se înmoaie în cazul în care este instalat pulverizatorul de benzină.
Viteza aerului din această secțiune crește, iar presiunea scade conform ecuației Bernoulli.
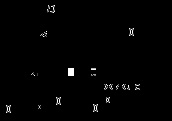
Am găsit acum o corelație între greutatea și consumul de benzină Gb vozduhaGv la razmerahD dat și coeficienții d și cu pro-TIV-ment al canalului de aer (până pct 2-2) și zhiklerazh v.
Se scrie ecuația Bernoulli pentru debitul de aer (secțiunile 0-0 și 2-2) și apoi pentru fluxul de benzină (secțiunile 1-1 și 2-2) și obținem pentru
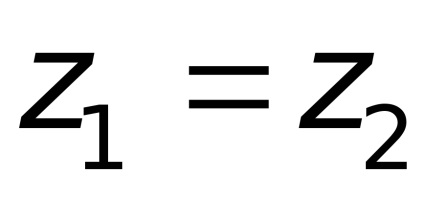
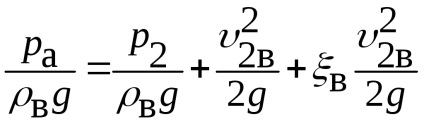
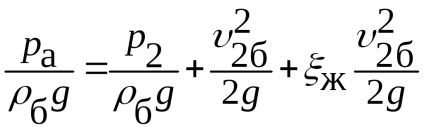
.
Luând în considerare costurile de greutate
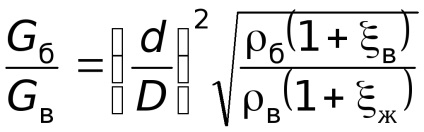
Exemplul 3 Tubul Pitot este folosit pe scară largă pentru măsurarea vitezei apei și gazului. Formăm ecuația Bernoulli pentru secțiunile 1-1 și 2-2. Planul orizontal de comparație 0-0 trece prin vârful tubului (Figura 3.15)
.
deoarece
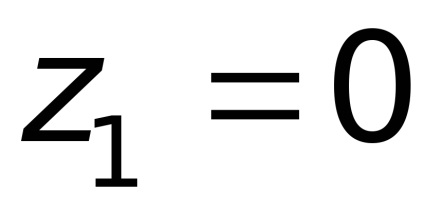
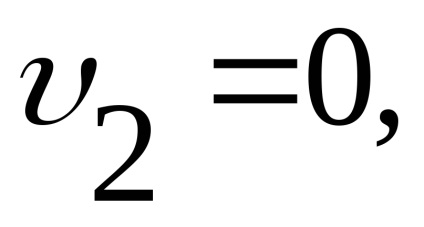
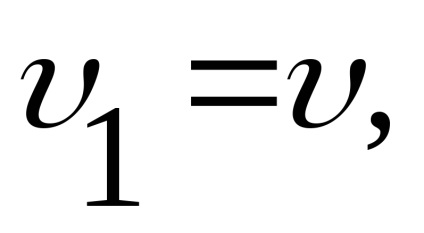

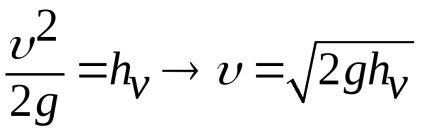
Întrebări de test
1. Scrieți ecuația Bernoulli pentru o scurgere elementară a fluidului invizibil și explicați cantitățile care intră în el.
2. Care este diferența dintre ecuația Bernoulli pentru curgerea unui fluid real din ecuația Bernoulli pentru o scurgere elementară?
3. Care este energia specifică totală a fluxului?
4. Explicați semnificația fizică a coeficientului Coriolis în ecuația Bernoulli.
5. Explicați semnificația energetică a ecuației Bernoulli.
6. Ce se numește gradienți piezometrici și hidraulici?
7. Dați exemple de aplicare practică a ecuației Bernoulli.
8. Pe baza cărui model a fost derivarea ecuației Bernoulli pentru fluxul unui lichid real
9. Ce este piezometrul și capul de mare viteză?
Ce se numește presiune totală?
3.12. Rezistența hidraulică. Moduri de mișcare fluide
Odată cu mișcarea lichidelor reale din diverse sisteme hidraulice, este necesară o evaluare precisă a pierderilor de presiune pentru depășirea rezistențelor hidraulice. Contabilizarea exactă a acestor pierderi determină în multe privințe fiabilitatea calculelor tehnice. În plus, ne permite să găsim o soluție tehnică viabilă din punct de vedere economic, care are un grad suficient de perfecțiune. Pentru aceasta, este necesar să avem o idee clară despre mecanismul de mișcare a lichidului.
În procesul de cercetare, faimosul fizician Reynolds în 1883 a confirmat teoria existenței a două regimuri de mișcare a lichidului. Acesta este în primul rând un regim laminar de mișcare a lichidului, corespunzător vitezelor reduse. Mișcarea laminară poate fi considerată ca mișcarea straturilor individuale de lichid, care are loc fără amestecarea particulelor.
La viteze mai mari ale fluidului, se observă un regim turbulent ("turbulența" în latină - vortex). Această mișcare este numită dezordonată.
Pentru a estima mișcarea fluidă, Reynolds a introdus un criteriu fără dimensiuni Re, care ține cont de efectul vitezei

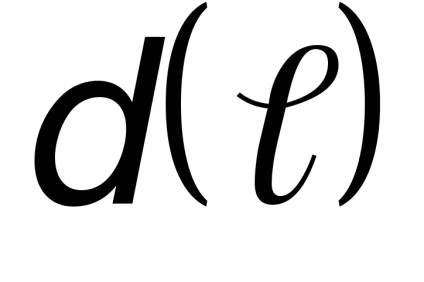
Limita existenței unui mod particular de mișcare a unui lichid este determinată de două valori critice ale numărului Re: cea mai mică


Astfel, când