1. Oscilație armonică.
Modelul matematic al unei oscilații armonice are forma:
u (t) = Ums sin (# 969; st + # 966; s) (11)
După cum se poate observa din modelul matematic, în spectrul acestei oscilații există o componentă armonică care se află pe frecvența # 969; s. Înălțimea componentei în spectrul de amplitudine este egală cu amplitudinea Ums de oscilație, iar în spectrul de fază - până la faza inițială a oscilației # 966; s. Mai mult decât atât, în construcția spectrului, este necesar să se ia în considerare legătura dintre diagrama timpului semnalului și spectrul de amplitudine. Amplitudinea componentei spectrului trebuie să corespundă în înălțime cu amplitudinea oscilației din diagrama timpului.
Trebuie notat că, pe măsură ce frecvența semnalului crește, componenta sa va fi îndepărtată de-a lungul axei de frecvență de la zero (Figura 13).
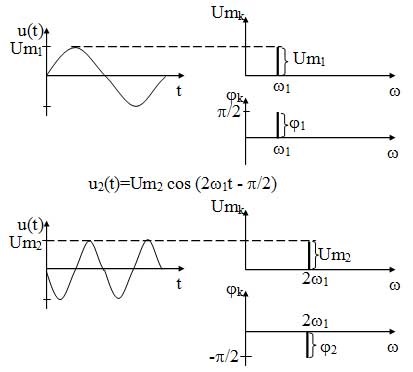
Figura 13 - Reprezentarea spectrală a oscilațiilor armonice
Așa cum se poate observa din figuri, spectrul unei oscilații armonice este discret și limitat.
2. Semnale periodice, non-armonice.
Principala caracteristică a reprezentării spectrale a acestor semnale este prezența în spectrul lor a unui set de componente spectrale. Astfel de semnale pot fi descrise de seriile Fourier, conform cărora:
adică semnalul poate fi reprezentat de suma componentei constante și a setului de componente armonice.
Transformăm această serie folosind proprietatea trigonometrică
sin (x + y) = sin x cos y + cos x sin y (13)
Presupunând că x = # 966; k și y = k # 969; ct, obținem:
De vreme ce Umk și K sunt parametrii seriei, atunci ele pot fi notate cu coeficienții
Umk păcătos # 966; k = ak; Umk, da (96); k = bk (15)
Apoi seria va arata astfel:
Parametrii seriei pot fi determinate în termeni de coeficienți ak și bk:
Amplitudinea componentei constante și a coeficienților poate fi determinată prin valoarea semnalului u (t):

O serie care, în cazul în care semnalul este descris de o funcție chiar f (t) = f (t), atunci seria va avea doar componentele cosinus ca bk = 0, în cazul în care o funcție impar (f (t) ≠ f (t) ), atunci rad conține doar componente sinusoidale (ak = 0).
Să luăm în considerare reprezentarea spectrală a semnalelor periodice, non-armonice folosind exemplul unei secvențe periodice de impulsuri dreptunghiulare (PPPI).
La construirea spectrului, trebuie calculați următorii parametri:
a) ciclul de funcționare:
b) valoarea componentei constante:
c) frecvența primei armonici a spectrului, care este egală cu frecvența semnalului:
d) amplitudinile componentelor armonice ale spectrului:
La construirea spectrului, este necesar să se ia în considerare următoarele caracteristici:
1. Toate componentele armonice sunt la frecvențe care sunt multipli ai frecvenței fundamentale (969 # 2; 1, 3 # 969; 1, 4 # 969; 1, etc ...);
2. Pentru spectrul de amplitudine:
a) spectrul PPPI are un caracter petale, adică un număr de "petale" se pot distinge în spectru;
b) numărul componentelor armonice din lob este dependent de raportul de sarcină și este egal cu q - 1;
c) amplitudinile componentelor armonice la frecvențele multiple ale ciclului de funcționare sunt zero;
d) forma spectrului este marcată de plic - o linie punctată, care leagă liniștit vârfurile componentelor armonice;
e) punctul din care emană plicul este 2U0 sau 2I0.
3. Pentru spectrul de fază:
a) toate componentele armonice, la frecvențe care nu sunt multipli ale ciclului de funcționare, au aceeași înălțime egală cu π / 2 (90 °);
b) toate componentele armonice din același lob au același semn, iar în cele opuse.
c) componentele la frecvențele mai multor cicluri de sarcină au o fază inițială egală cu zero.
Spectrele PPPI la ciclul de sarcină q = 3 sunt prezentate în figura 14.
După cum se poate observa din diagrame, spectrul PPPI este discret și nelimitat. Prin urmare, pentru lărgimea spectrului, se ia intervalul de frecvență în care sunt localizate primele două lobi, deoarece acestea conțin circa 95% din energia semnalului:
# 916; fs = 2 / # 964; (26)
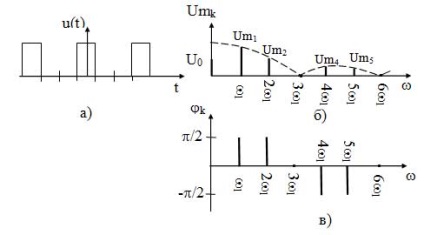
Figura 14 - Reprezentarea spectrală a RFP: a) diagrama timpului; b) diagrama de amplitudine spectrală; c) diagrama de fază spectrală
După cum se poate observa din formula, lățimea spectrului PPIS depinde doar de durata impulsului și nu depinde de perioada sa.
3. Semnale neperiodice.
Deoarece semnalele neperiodice nu se poate selecta perioada t. K. T → ∞, apoi se calculează și se trasează spectrul prin aceeași metodă ca și că este imposibil pentru semnale periodice. Cu toate acestea, cunoașterea spectrului acestor semnale este necesar, adică. K. Toate semnalele de informație sunt non-periodice. Pentru a construi un spectru semnal nonperiodic produs următoarea procedură: semnal mental ca un lot cu o perioadă arbitrară, care construiesc ddlya spectru. Apoi, procesul de limitare a perioadei infinit lăsa (T → ∞) (Figura 15). Frecvența primei armonici și, în consecință, distanța dintre componentele armonice tind spre zero (f1 = 1 / T), astfel încât toate componentele îmbinare între ele și formează un spectru continuu.
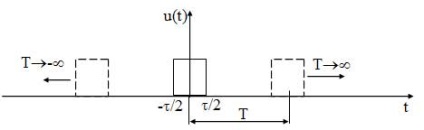
Figura 15 - Semnalul impulsului u (t) și reprezentarea acestuia printr-un semnal periodic
Forma spectrului de semnale neperiodice este indicată de plic (linia solidă) (Figura 16).
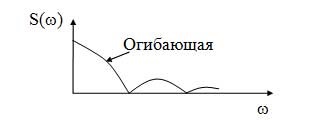
Figura 16 - Diagrama spectrala a unui semnal neperiodic
Seria Fourier, pentru asemenea semnale, nu poate fi scrisă, deoarece în acest caz amplitudinea componentei constante și coeficienții ak și bk sunt egale cu zero. În acest caz, valoarea semnalului în orice moment este, de asemenea, zero, ceea ce nu este adevărat. Prin urmare, pentru astfel de semnale se utilizează transformări Fourier:
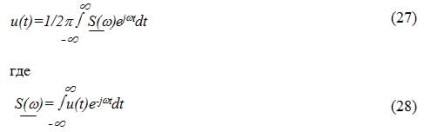
Expresia (27) este transformarea inversă și (28) este o transformare directă Fourier.
Cantitatea S (# 969;) este densitatea spectrală complexă a semnalului neperiodic u (t). Este egal cu:
unde S (# 969;) este densitatea spectrală a amplitudinii sau spectrul de amplitudine al semnalului neperiodic și (# 969;) - spectrul de fază al semnalului neperiodic.
Densitatea spectrală a amplitudinii unui semnal nonperiodic la orice frecvență # 969; este egal cu amplitudinea totală a componentelor într-o bandă mică # 916; # 969; în apropierea frecvenței # 969; numărate pentru 1 Hertz.
Diagramele de timp și densitatea spectrală a amplitudinilor pentru impulsurile rectangulare și triunghiulare sunt prezentate în figura 18:
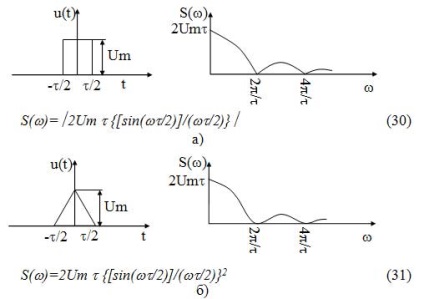
Figura 18 - Reprezentarea spectrală a semnalelor neperiodice: a) impuls dreptunghiular; b) un impuls triunghiular