Fig. 3. Podurile Cone Koenigsberg
Modificăm problema într-o oarecare măsură. Fiecare dintre zonele considerate, separate de un râu, indicăm cu un punct, iar punțile care le conectează sunt un segment de linie (nu neapărat o linie dreaptă). Apoi, în loc de plan, vom lucra pur și simplu cu o anumită figură compusă din segmente de curbe și linii. Astfel de figuri din matematica modernă se numesc grafuri, segmentele sunt coaste, iar punctele care leagă marginile sunt vârfuri. Apoi, problema inițială este echivalentă cu următoarea: dacă este posibilă trasarea unui graf dat fără a lua creionul din hârtie, adică în așa fel încât fiecare dintre margini să treacă exact o dată.
Astfel de grafice care pot fi trase fără a ridica creionul de hârtie, numit unicursal (de la Cursus Unus Latină - un fel) sau Euler. Deci, sarcina este pusă astfel: în ce condiții este graficul unicursal? În mod evident, graficul unicursal nu încetează să mai fie unicursal, dacă modificați lungimea sau forma coastele lui, și de a schimba locația nod - dar nu ar schimba blaturi de conectare coaste (în sensul că, dacă sunt conectate două vârfuri, acestea trebuie să fie conectate, iar dacă ar fi întreruptă Apoi deconectat).
Fig. 4. Grafice echivalente topologic
Dacă graficul este unicursal, atunci graficul echivalent topologic este, de asemenea, unicursal. Prin urmare, unicurismul este o proprietate topologică a graficului.
În primul rând, este necesar să se facă distincția între graficele conectate și cele deconectate. Sunt conectate astfel de figuri încât orice două puncte pot fi conectate într-un fel care aparține acestei figuri. De exemplu, majoritatea literelor din alfabetul rusesc sunt legate, dar litera Y nu este: este imposibil să mergeți de la jumătatea stângă la dreapta, prin punctele care aparțin acestei scrisori. Conectivitatea este o proprietate topologică: nu se schimbă atunci când se transformă o figură fără spargere și lipire. Este clar că dacă graficul este unicursal, atunci trebuie să fie conectat.
În al doilea rând, ia în considerare vârfurile graficului. Vom numi indexul vârfului numărul de margini întâlnite la acest vârf. Acum, să ne întrebăm: ce poate fi egal cu indicele vârfurilor grafului unicursal.
Poate începe și se termină în același punct (să-l numim „traseu închis“), linia este trasată grafic, și poate fi în diferite (o numim „cale non-închis“): Pot exista două cazuri. Încercați-l pentru tine pentru a trage o astfel de linie - ceea ce doriți să se auto-intersecții - .. duble, triple, etc. (pentru claritate, este cel mai bine să coaste nu au fost mai mult de 15).
Este ușor de observat că într-un mod închis toate nodurile au chiar indicii, și într-un deschis - exact două sunt ciudat (acest lucru este începutul și sfârșitul drumului). Faptul este că, în cazul în care nodul nu este un început sau sfârșit, a venit la el, noi trebuie să fim apoi din ea - atât cât de multe margini sunt incluse în ea, la fel de mult din ea, ci doar numărul de muchii de intrare și de ieșire este chiar . Dacă vârful inițial coincide cu vârful finit, atunci și indicele său este chiar: de câte marginile ieșite din el, după cum au intrat mulți. Și dacă punctul inițial nu coincide cu sfârșitul anului, indicii lor ciudat: de la punctul de plecare trebuie să obțină o dată afară, și apoi, dacă se întoarce și apoi pleacă din nou în cazul în care din nou - să plece din nou, etc;.. iar ultimul trebuie să vină, și dacă îl lăsăm mai târziu, atunci din nou trebuie să ne întoarcem și așa mai departe.
Pentru ca graficul să fie unicursal, este necesar ca toate nodurile lui să aibă un indice par, sau că numărul de noduri cu un indice ciudat este egal cu două.
Acum, uita-te din nou la graficul problemei podurilor Koenigsberg.
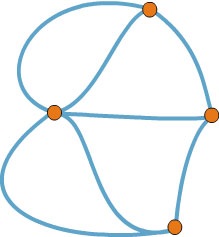
Fig. 5. Podurile Cone Koenigsberg
Contorizați indicii vârfurilor și asigurați-vă că nu poate fi unicursal în nici un fel. De aceea nu ați reușit când ați vrut să ocoliți toate podurile.
Se pune întrebarea: dacă nu există noduri cu un indice ciudat într-un grafic conectat sau dacă există exact două astfel de noduri, este graficul în mod necesar unicursal? Puteți dovedi cu strictețe că da! Astfel, unicursalitatea este în mod unic legată de numărul de vârfuri cu un indice ciudat.
Exercițiu: Construiți pe schema de Königsberg pod un alt pod - oriunde doriți - că podurile rezultate ar putea fi eludate, vizitând fiecare exact o dată; într-adevăr face acest lucru.
Iată câteva grafice - numărați indicii de la vârf și, dacă este posibil, încercați să le ocoliți "fără a lua creionul din hârtie".
Model 1. Grafice unicursale
Acum, un fapt mai interesant: se dovedește că orice sistem de zone legate de poduri poate fi bypassed dacă este necesar să vizitați fiecare pod exact de două ori! Încearcă să-l dovedești singur.
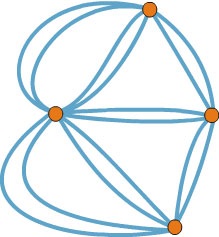
Fig. 6. Podurile Koenigsberg cu dublul numărului de poduri unicuristice