Problema 1. Un bord de diapozitive de masă r de-a lungul unui fir vertical. Determinați accelerația talonului și tensiunea firului, dacă forța de frecare dintre talon și firul H. Care ar trebui să fie forța de frecare astfel încât talonul să nu alunece firul?
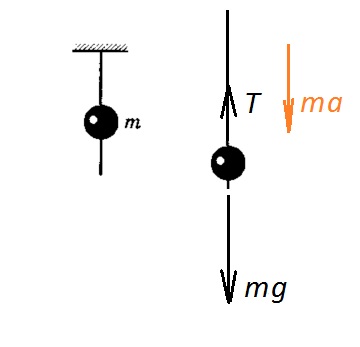
Să scriem cea de-a doua lege a lui Newton pe proiecții pe axa verticală, pe care o indicăm în sus:
Că mărgelele nu alunecă, este necesar
Tensiunea firului este egală cu forța cu care coroana acționează asupra firului - și aceasta este forța de frecare:
Răspuns: m / s. N, N.
Problema 2. O bară cu o masă kg este fixată între două planuri verticale cu forța H. Găsiți accelerația barei și forța de frecare dintre bara și planul atunci când aceasta alunecă. Care este forța verticală minimă pe care trebuie să o atașați la bar, astfel încât: a) să nu vă alunecați; b) ridica? Coeficient de frecare.
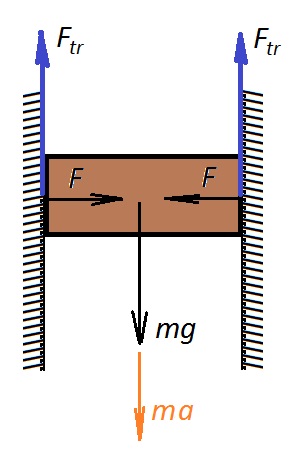
La început bara este pur și simplu fixată, dar nu atât de puternică încât să o țină în continuare. Prin urmare, el va aluneca: se mută în jos. Să găsim accelerația (axa este îndreptată în sus):
Forța de frecare este luată în considerare de două ori, deoarece bara se freacă deopotrivă pereții din stânga și din dreapta. Rezistența reacției de susținere este forța cu care bara este fixată:
Pentru a împiedica alunecarea barei, este necesar ca accelerarea sa să fie zero. Apoi, forța de frecare ne ajută să ținem bara și să îndreptăm în sus.
Acum trageți bara în sus. Pe măsură ce bara se deplasează în sus, forța de frecare trebuie îndreptată în jos:
Răspuns: m / s. N, N.
Sarcina 3. O funie este aruncată printr-o grindă staționară, orizontală, la o anumită înălțime. Pentru a menține o sarcină de kg greutată suspendată de la un capăt al cablului, este necesar să trageți cel de-al doilea capăt al cablului cu o forță minimă H. Determinați forța minimă. cu care este necesar să trageți frânghia astfel încât sarcina să înceapă să crească.
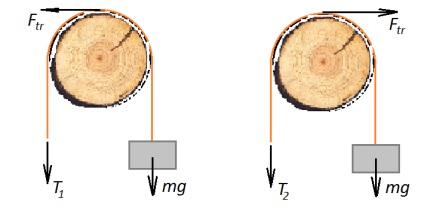
Să analizăm mai întâi situația în care încărcătura este ținută pur și simplu pe o funie, aruncată peste un jurnal, într-o stare suspendată. În acest caz, frânghia se va freca de arbore, ca rezultat, forța de frecare rezultată ne ajută să menținem sarcina, adică,
Acum vom trage frânghia, ridicând încărcătura. În acest caz, forța de frecare acționează împotriva noastră: trebuie să o depășim.
Problema 4. Un magnet de masă kg este atras de perete cu forța H. Dacă aplicăm o altă forță H magnetului, care face un unghi cu peretele, atunci unde și cu ce accelerație se va mișca magnetul? Coeficientul de frecare dintre perete și magnet. La ce valori nu se va mișca magnetul?
Deoarece forța este îndreptată în sus, presupunem că magnetul se mișcă și în sus cu accelerația. Direcționăm axa în sus și scriem ecuația conform celei de-a doua legi a lui Newton:
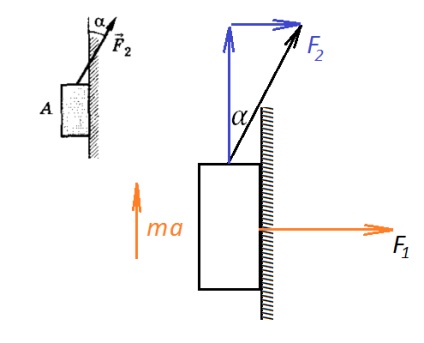
Forța cu care se apasă magnetul împotriva peretelui este
Iar forța de frecare este atunci
Apoi, accelerația magnetului este:
Am primit o accelerație negativă, deci presupunerea că mișcarea magnetului este incorectă. Trebuie să re-scriem ecuația luând în considerare acest fapt. apoi:
Apoi accelerația magnetului va fi:
Dacă accelerația este zero, atunci magnetul este staționar (poate fi fixat). În această condiție, coeficientul de frecare este:
Răspuns: accelerația magnetului m / s. orientat în jos, coeficientul de frecare care asigură imobilitate.