Forma parabolei. Ecuația unei parabole. Parabola este determinată în mod unic de focalizarea ei F și de direcția directrix f. Perpendicularul x ≡ FD. omisă din focalizarea pe directrix, se numește axa parabolică, iar distanța p de la focalizare la directrix este parametrul său (vezi figura 1).
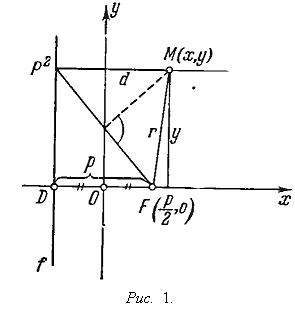
De la definirea unei parabole ca locus geometric de puncte echidistant de la F și f. rezultă că parabola este simetrică față de axa proprie. iar axa x are un singur punct comun O - punctul mijlociu al segmentului FD - cu parabola. Punctul O se numește vârful parabolei.
Trasează prin punctul O linia dreaptă y. perpendicular pe axa x. Evident, în plus față de punctul O pe linia y nu există alte puncte ale parabolei, deoarece pentru fiecare punct P al liniei y. care este diferită de O. Distanța r la focalizare este mai mare, distanța PP1 = d la direcția directă este egală cu și, prin urmare, r. d> 1, adică punctul P nu aparține parabolei. Pentru fiecare punct P al planului situat cu focalizarea F pe laturile opuse ale directrix, r> d. și de aceea nu există nici o parabolă în acest jumătate de plan. În consecință, punctele de parabolă sunt situate pe cealaltă parte a liniei y. cu care se află centrul parabolei. Prin simetrie, orice linie dreaptă paralelă cu linia y și având un punct comun cu parabola are un alt punct comun cu ea și numai linia dreaptă y are un punct comun cu o parabolă. Drept urmare, linia dreaptă y este numită tangentă la parabola la vârful ei.
Să luăm acum axa parabolei x ca fiind abscisa, iar tangenta y la vârf ca axa ordonată a sistemului de coordonate dreptunghiulare. Fie M (x, y) un punct arbitrar al parabolei (vezi Figura 1). atunci
iar din egalitatea r 2 = d 2 rezultă că
Forma parabolei, ecuația parabolică, axa și parametrul parabolei, tangentă la parabola și vârful ei.