Descrierea prezentării pe diapozitive individuale:
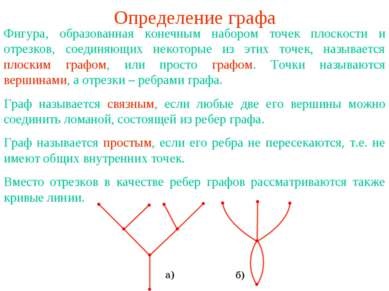
Definirea unui grafic O cifră formată dintr-un set finit de puncte ale unui plan și segmente care unește unele dintre aceste puncte se numește un grafic plat sau pur și simplu un grafic. Punctele sunt numite noduri, iar segmentele sunt numite marginile graficului. Se spune că un grafic este conectat dacă vreunul dintre vârfurile acestuia poate fi îmbinat printr-o linie poligonală formată din muchiile graficului. Se spune că un grafic este simplu dacă marginile sale nu se intersectează; nu au puncte comune comune. În loc de segmente, liniile curbe sunt, de asemenea, considerate ca marginile grafurilor.
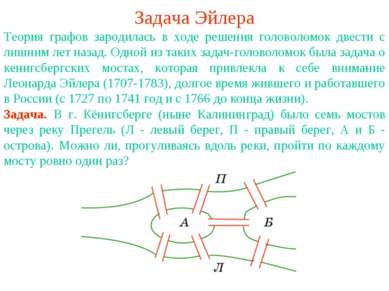
Problema lui Euler Teoria grafurilor a apărut în soluția de puzzle-uri de peste două sute de ani în urmă. O astfel de problemă de puzzle a fost problema podurilor din Königsberg, care a atras atenția Leonhard Euler (1707-1783), o lungă perioadă de timp a trăit și a lucrat în Rusia (1727-1741 și de la 1766 până la moartea sa). Sarcina. În orașul Königsberg (Kaliningrad acum) a avut șapte poduri peste râul Pregelul (L - mal stâng, R - malul drept, A și B - a insulei). Este posibil, mergând de-a lungul râului, să treacă prin fiecare pod exact o dată?
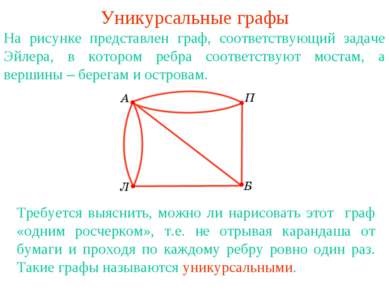
Grafice unicursale Figura prezintă un grafic care corespunde problemei Euler, în care marginile corespund punților, iar nodurile către țărmuri și insule. Este necesar să aflăm dacă acest grafic poate fi desenat "într-o singură lovitură", adică Nu rupeți creionul de pe hârtie și treceți prin fiecare margine exact o dată. Astfel de grafice sunt numite unicursal.

Teorema Indicele unui vârf al unui grafic este numărul de muchii convergente la acest vârf (marginile, cu începutul și sfârșitul la un vârf date sunt numărate de două ori). Teorema. Pentru un grafic unicursal, numărul de noduri ale unui indice ciudat este zero sau două. Dovada. Dacă graficul este unicursal, atunci are un început și un sfârșit al bypass-ului. Vârfurile rămase au un indice par, deoarece există o ieșire cu fiecare intrare într-un astfel de vârf. Dacă începutul și sfârșitul nu coincid, atunci ele sunt singurele noduri ale indexului ciudat. Începerea ieșirilor este mai mult decât intrările, iar la sfârșitul intrărilor există mai mult decât ieșirile. Dacă începutul coincide cu sfârșitul, atunci nu există noduri cu un indice ciudat. Conversia este, de asemenea, adevărată: dacă graficul conectat are un număr de noduri de indice egal cu zero sau două, atunci este unicursal.

Soluția problemei Euler Soluția problemei Euler. Să găsim indicii vârfurilor graficului problemei Euler. Vârful A are indicele 5, B - 3, P - 3 și A - 3. Astfel, avem patru noduri de indice ciudat și, prin urmare, graficul dat nu este unicursal. Prin urmare, nu puteți trece prin fiecare dintre cele șapte poduri o singură dată.

Întrebarea 1 Ce figura se numește grafic? Răspuns: Un grafic este o figură formată dintr-un set finit de puncte ale unui plan și segmente care leagă unele dintre aceste puncte.

Întrebarea 2 Ce grafic este numit unicursal? Răspuns: Un grafic este numit unicursal dacă poate fi desenat "într-o singură lovitură", adică Nu rupeți creionul de pe hârtie și treceți prin fiecare margine exact o dată.

Întrebarea 3 Care este indicele vârfului unui grafic? Răspuns: Indicele unui vârf al unui grafic este numărul de muchii convergente la acest vârf (marginile cu un început și un capăt la un vârf dat sunt numărate de două ori).

Întrebarea 4 Ce se întâmplă cu indicele vârfurilor unui grafic unicursal? Răspuns: Pentru un grafic unicursal, numărul de vârfuri ale unui indice ciudat este zero sau două.
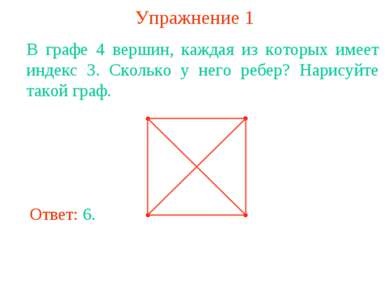
Exercitarea 1 În coloana 4 a vârfurilor, fiecare dintre ele având un indice de 3. Câte margini are? Desenați un astfel de grafic.
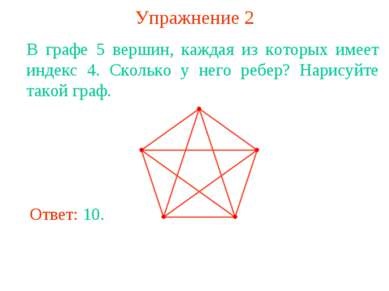
Exercițiul 2 În coloana 5 de noduri, fiecare dintre ele având un index de 4. Câte margini are? Desenați un astfel de grafic.
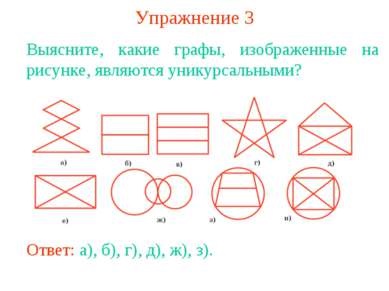
Exercițiul 3 Aflați care dintre graficele afișate în figură sunt unicursal? Răspunsul este: a), b), d), e), g), h).

Exercițiul 4 Un grafic poate avea: a) un vârf al unui indice ciudat; b) două noduri de indice ciudat; c) trei noduri de indice ciudat; d) patru noduri ale unui indice ciudat? Răspunsul este: a), c) Nu; b), d) da.
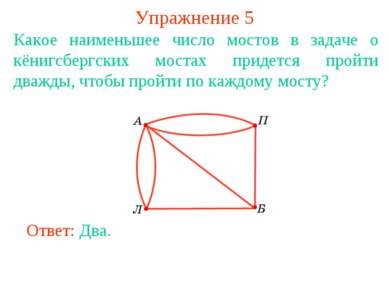
Exercițiul 5 Care este cel mai mic număr de punți din podul Koenigsberg care urmează să fie traversat de două ori pentru a trece prin fiecare pod? Răspuns: Doi.
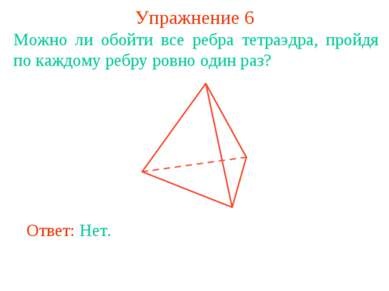
Exercitiul 6 Este posibil sa ocoliti toate marginile unui tetraedru, trecand fiecare margine exact o data? Răspuns: Nu.
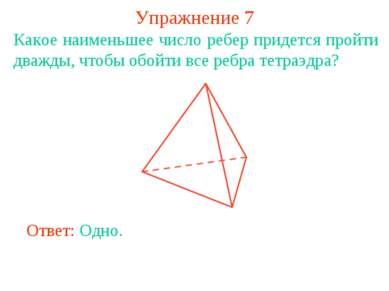
Exercițiul 7 Care dintre cele mai puține margini trebuie să treceți de două ori pentru a obține toate marginile tetraedrului? Răspuns: Unul.

Exercitiul 8 Care dintre cele mai putine margini trebuie sa treci de doua ori pentru a obtine toate marginile tetraedrului si a te intoarce la versantul original? Răspuns: Doi.
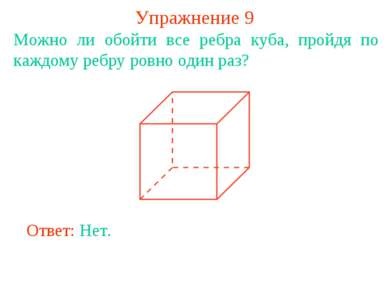
Exercițiul 9 Este posibil să vă apropiați de toate marginile unui cub trecând prin fiecare margine exact o dată? Răspuns: Nu.
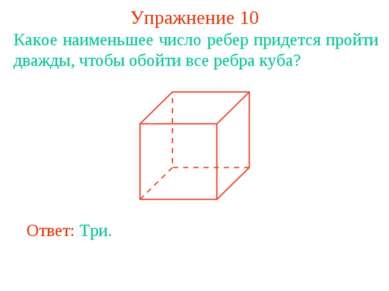
Exercitiul 10 Care dintre cele mai putine margini trebuie sa treci de doua ori pentru a obtine toate marginile cubului? Răspuns: Trei.
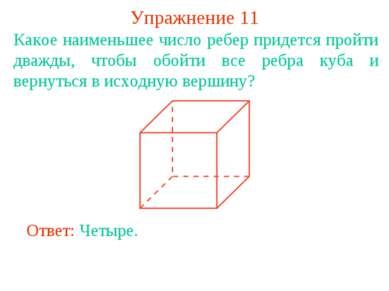
Exercitarea 11 Care dintre cele mai putine margini trebuie sa treci de doua ori pentru a obtine toate marginile cubului si pentru a reveni la versantul original? Răspuns: Patru.
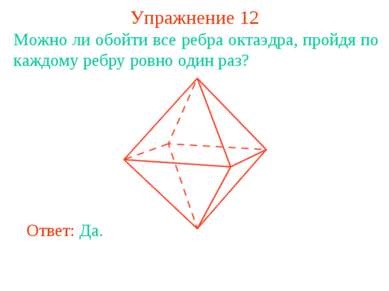
Exercitarea 12 Este posibil să ocolească toate marginile unui octaedru, trecând fiecare margine exact o dată? Răspuns: Da.

Exercitarea 13 Este posibil să ocolească toate marginile unui icosaedru, trecând fiecare margine exact o dată? Răspuns: Nu.

Exercițiul 14 Care dintre cele mai puține margini trebuie să treceți de două ori pentru a vă deplasa pe toate marginile icosahedronului? Răspuns: Cinci.

Exercițiul 15 Care dintre cele mai puține margini trebuie să treceți de două ori pentru a vă deplasa pe toate marginile icosahedronului și pentru a reveni la versantul original? Răspuns: Șase.
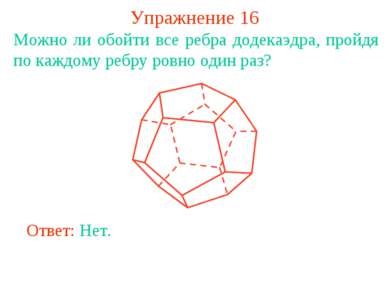
Exercitarea 16 Este posibilă ocolirea tuturor marginilor unui dodecaedru, trecând fiecare margine exact o dată? Răspuns: Nu.
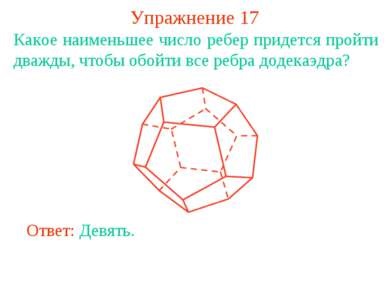
Exercitiul 17 Care dintre cele mai putine margini trebuie sa treci de doua ori pentru a obtine toate marginile dodecaedrului? Răspuns: Nouă.
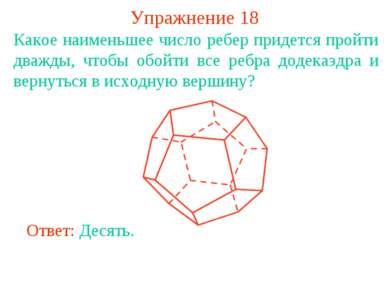
Exercițiul 18 Care dintre cele mai puține margini trebuie să treci de două ori pentru a trece prin toate marginile dodecahedronului și pentru a reveni la versiunea originală? Răspuns: Zece.
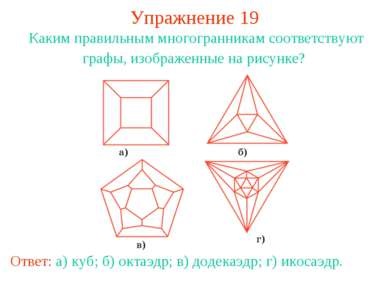
Exercitarea 19 Ce poliedru obișnuit corespunde graficelor prezentate în figură? Răspunsul este: a) cub; b) octaedrul; c) un dodecaedru; d) icosaedrone.
Prezentări înrudite

Model și portofoliu de fotografi

Identificarea speciilor de animale și a păsărilor din jurul satului Hani, a habitatului acestora, în funcție de caracteristicile naturale și climatice ale zonei

Determinarea conținutului de iod în produsele alimentare

Determinarea forței de frecare a culiselor

Determinarea cantitativă a vitaminei C în produsele alimentare prin metoda iodometrică

Definirea rolului unui câine în istoria societății umane și percepția sa în diferite tradiții etno-culturale

Grafice. Gradul de vârf. Numărarea numărului de margini ale unui grafic

Autodeterminarea elevilor unei școli de limbi străine în profesia viitoare
7311 7866 7998 9579 9630 9867 10685 11581
Prezentări pentru lecția Geometrie

Sinus, cosinus, tangent de clasa unghiulară 9

Simptomele unui paralelogram

Simetria - în jurul nostru

sarcinile de examen de admitere


Construcții geometrice folosind o busolă și o riglă


„Risc“


poliedre

axiala și simetria centrală

Vizualizați toate prezentările după geometrie
32685 32738 32752 32898 32920 33141 33503 33504 33522 33751 33939 34145