2,24. Convoluția liniară a secvențelor finite
Considerăm două secvențe finite și lungimi în ceea ce privește eșantioanele, adică este diferită de zero pentru, a - pentru. Convoluția liniară sau aperiodică a acestor secvențe este o secvență definită de relație
unde și sunt zero în afara intervalelor corespunzătoare. În Fig. 2.30 prezintă exemple de secvențe și. Este clar că secvența este finită și are o lungime de citire.
Deasupra sa arătat că înmulțirea DFT a două secvențe finite și găsirea inverse DFT a produsului, obținem același rezultat ca convoluția circulară secvențe periodice echivalente derivate din secvențe de date finite. Pe baza acestei (a se vedea. De asemenea, exemplul din fig. 2.29), se pot obține sinuozitate destul simplu liniară a două secvențe finite. Sinuozitate secvență periodică este periodică și are aceeași perioadă ca și secvențele înseși. Deoarece perioada convoluție (Fig. 2.30) este numărul de egal, pentru a obține o astfel de perioadă în convoluția circulară este necesar ca conținea probe din această complement atins fiecare dintre cele două secvențe număr de exemple zero corespunzătoare. După aceasta se găsește DFT augmented secvențe litera de multiplica și de a efectua produsul inverse DFT.
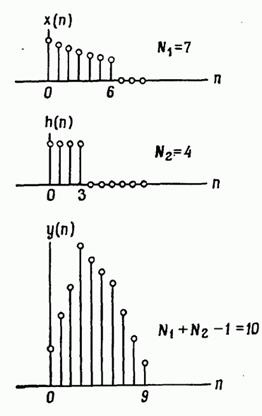
FIG. 2.30. Convoluția liniară (aperiodică).
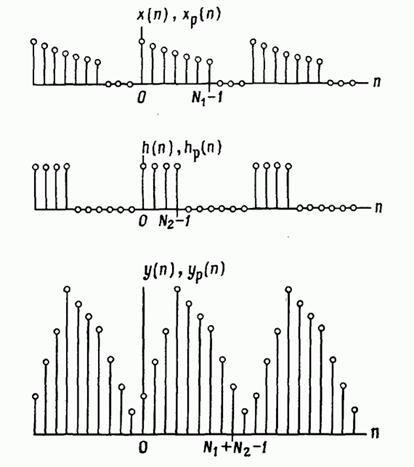
FIG. 2.31. Calcularea convoluției liniare prin convoluție circulară.
Rezultatul este convoluția dorită. În Fig. 2.31, care ilustrează aceste operații, sunt afișate secvențele periodice echivalente utilizate în calculul convoluției circulare. Este clar că adăugarea de secvențe inițiale de lungime finită și numărătoare zero aduce perioada la valoarea dorită și permite eliminarea suprapunerilor circulare caracteristice convoluției circulare. Ca urmare, fiecare perioadă a secvenței (Figura 2.31) coincide cu (Figura 2.30). Metoda considerată pentru calcularea convoluției a două secvențe finite folosind algoritmul DFT se numește convoluție rapidă, spre deosebire de metoda calculului direct al sumei (2.165), numită convoluție directă sau lentă. Termenul "rapid" este folosit deoarece DFT poate fi calculat rapid și eficient utilizând unul dintre algoritmii FFT (Fast Fourier Transform). Se poate arăta că, chiar și cu valori moderate (de exemplu, de ordinul a 30), o convoluție rapidă este mai eficientă decât o linie dreaptă. Prin urmare, această tehnică este un instrument important de calcul pentru procesarea semnalelor.
Pentru aplicațiile practice, este important de observat că în exemplul considerat mai sus dimensiunea DFT nu este neapărat limitată de magnitudine. DFT poate fi efectuat pentru orice număr de probe care satisfac starea. Dacă această condiție este satisfăcută, atunci, spre deosebire de tehnica descrisă mai sus, secvențele sunt completate de un alt număr de eșantioane zero. Ca rezultat, secvența periodică echivalentă va avea zero la sfârșitul perioadelor. Este clar că aceste diferențe nu distorsionează rezultatul dorit în nici un fel. Posibilitatea alegerii arbitrare este semnificativă, deoarece algoritmii practici pentru calculul DFT pentru diferiți au eficacitate diferită. De exemplu, pentru unele algoritmi este necesar să fie egal cu o putere de 2. În acest caz, în calitate este necesar să alegeți un număr egal cu puterea de 2 și nu mai puțin de.