Curs 15. Construirea regiunilor de stabilitate. Conceptul de descompunere D
Construcția regiunilor de stabilitate și a descompunerii D sunt folosite pentru a studia influența valorilor parametrilor sistemului asupra stabilității și calității acestuia.
Domeniul stabilității în spațiul parametrilor sistemului (coeficienții de transmisie, constantele de timp ale legăturilor sistemului etc.) este domeniul parametrilor la care sistemul este stabil.
Limitele regiunii de stabilitate corespund limitelor de stabilitate ale sistemului:
- aperiodic (prezența unei rădăcini zero a polinomului caracteristic) obținută prin condiția că termenul liber al polinomului caracteristic este zero, a = 0;
- corespunzând rădăcinii infinite a polinomului caracteristic obținut prin condiția a0 = 0;
- vibrațional (prezența unei perechi de rădăcini imaginare ale polinomului caracteristic) derivate din condițiile Dn-1 = 0, în conformitate cu criteriul Hurwitz, D (j w) = 0, în conformitate cu criteriul Mikhailova sau W (j w) = - 1, în conformitate cu criteriul Nyquist.
De interes practic este construirea unei regiuni de stabilitate în planul a doi parametri aleși din setul de parametri ai sistemului, în conformitate cu trăsăturile problemelor care trebuie rezolvate. Principalul mod de construire implică utilizarea criteriului de stabilitate al lui Mikhailov.
Este introdus sistemul de coordonate 0AB. unde valorile parametrilor sistemului A și B sunt reprezentați grafic pe axe.
Coeficienții polinomului caracteristic al unui sistem închis
sunt exprimate în termeni de valori ale acestor parametri.
Pentru a obține ecuațiile limitelor regiunii de stabilitate, ecuațiile sunt construite în conformitate cu condițiile enumerate mai sus.
Principala complexitate în construirea regiunii de stabilitate este legată de construirea unei curbe corespunzătoare limitei de stabilitate a vibrațiilor. În conformitate cu criteriul lui Mihailov pentru producția sa, se compune un sistem de ecuații:
, unde X și Y sunt părțile reale și imaginare ale complexului caracteristic D (j w). Soluția sa ne permite să obținem ecuațiile parametrice ale curbei cerute în forma A = A (w), B = B (w). O excepție de la aceste ecuații de frecvență poate fi obținută în forma obișnuită B = B (A).
După ce a găsit limitele regiunii de stabilitate, se determină locația acesteia. Pentru limitele primului și celui de-al treilea tip, acest lucru se poate face direct pe baza condiției de stabilitate necesare. În regiunea de stabilitate, trebuie să se mențină a0> 0 și a> 0.
Se consideră un criteriu suplimentar pentru limita vibrațională. Un determinant al derivatelor parțiale
Dacă D> 0, atunci când se deplasează de-a lungul acestei limite în direcția creșterii frecvenței, regiunea de stabilitate este situată în stânga. Dacă D<0 - справа.
Regiunea de stabilitate construită este de obicei selectată prin ecloziune orientată spre interior.
De exemplu, construim regiunea de stabilitate pentru sistemul arătat în figura 88, în planul parametrilor k și T1.
Formăm polinomul caracteristic
și caracteristic complex
Să găsim limitele de stabilitate.
1. Limita aperiodică: an = k = 0. Regiunea de stabilitate corespunde k> 0.
2. Limita care corespunde unei rădăcini infinite: a0 = T1T2 = 0. Ca rezultat, ecuația limită este T1 = 0. Regiunea de stabilitate corespunde T1> 0.
3. Limita de vibrație:
Ca rezultat, obținem ecuațiile parametrice ale limitei vibraționale:
Acum excludem din ecuațiile obținute frecvența:
Curba corespunzătoare are forma unei hiperbola (Figura 111).
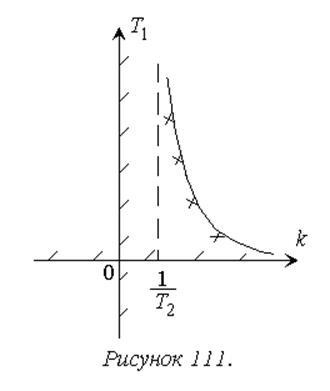
Să găsim locația regiunii de stabilitate în raport cu această limită, luând în considerare A = k. B = T1:
Pentru w> 0, o creștere a frecvenței de la 0 la ∞ corespunde mișcării de-a lungul limitei vibraționale, după cum rezultă din ecuațiile parametrice, în direcția creșterii k și scăderii T1. Mai mult, D<0, то есть область устойчивости расположена справа.
Pentru w<0 увеличению частоты от - ∞ до 0 соответствует движение по колебательной границе, как следует из параметрических уравнений, в обратном направлении. При этом D>0, adică regiunea de stabilitate este situată în partea dreaptă.
O partiție D este setul complet de curbe care împart planul parametrilor în regiuni cu distribuție diferită a rădăcinilor polinomului caracteristic D (s).