Înainte de a trece la studiul metodelor de reprezentare a unui grafic, luăm în considerare exemplele, oferim o definiție a graficului și cunoaștem conceptele de bază ale teoriei grafurilor. Toate aspectele teoriei grafurilor nu vor fi luate în considerare aici (acest lucru nu este necesar), ci, în cea mai mare parte, cele care vor fi necesare în viitor.
În viața noastră, într-un fel sau altul, suntem în contact cu obiecte care au o structură grafică. Astfel de obiecte includ diferite tipuri de rute de transport public: sistemul de metrou, rute de autobuz etc. În special, programatorul este familiarizat cu rețeaua de calculatoare, care este, de asemenea, un grafic (Figura 3.1). Frecvente aici este prezența punctelor conectate prin linii. Deci, într-o rețea de calculatoare, punctele sunt servere separate, iar liniile sunt diferite tipuri de semnale electrice. În metrou, primul este stația, al doilea este tunelurile așezate între ele. În teoria grafurilor, punctele sunt numite noduri sau vârfuri. și liniile de coaste sau arce. Astfel, un grafic este o colecție de vârfuri conectate de margini.
Să ne întoarcem la rețeaua de calculatoare. Are o anumită topologie și poate fi descrisă condiționat sub forma unui număr de calculatoare și a căilor lor de conectare. Figura de mai jos prezintă un exemplu de topologie complet conectată.
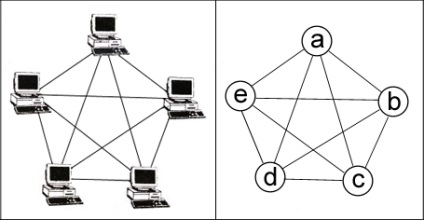
Figura 3.1 - Rețea de calculatoare
Acesta este, de fapt, un grafic. Cinci calculatoare sunt vârfuri și conexiuni (căi de semnalizare) între ele sunt coaste. Înlocuirea computerelor cu vârfuri obține un obiect matematic - un grafic care are 10 margini și 5 noduri. Puteți numerota vârfurile în mod arbitrar, și nu neapărat așa cum se face în figură.
Iată câteva notații importante folosite în teoria graficelor:
· | V | - ordinea (numărul de noduri);
· | E | - dimensiunea graficului (numărul de margini).
În cazul nostru (figura 1) | V | = 5, | E | = 10;
Atunci când orice alt vârf este accesibil din orice vârf, atunci un astfel de graf este numit un grafic neorientat (Figura 3.1). Dacă graficul este conectat, dar această condiție nu este îndeplinită, atunci un astfel de grafic este denumit un grafic orientat sau digraf (a se vedea Figura 3.2). Marginile unui digar sunt denumite în mod obișnuit arce.
În grafice orientate și nedirecționate există o noțiune a gradului unui vârf. Gradul unui vârf este numărul de muchii care îl conectează la alte noduri. Gradul de intrare a vârfului este numărul de margini care intră în acest vârf, gradul de ieșire fiind numărul de margini de ieșire. Suma tuturor gradelor graficului este de două ori numărul tuturor margini. Pentru Figura 2, suma tuturor puterilor este de 20.
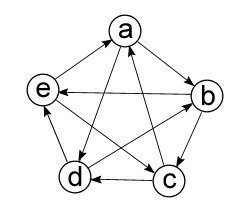
Figura 3.2 - Graficul orientat
Într-un digraph, spre deosebire de un grafic nedirecționat, este posibil să trecem de la vârful h la vârful s fără vârfuri intermediare, numai atunci când arcul frunze h și intră s. dar nu invers.
Graficele orientate au următoarea formă de înregistrare:
Al treilea tip de grafic este reprezentat de grafice mixte (Figura 3.3). Au ambele coaste direcționate și cele nedirecționale. Un grafic mixt formal este scris după cum urmează: G = (V.E.A), unde fiecare dintre litere în paranteze înseamnă de asemenea că a fost atribuită mai devreme.
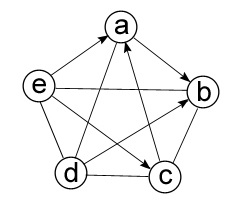
Figura 3.3 - Graficul mixt
Când ambele muchii coincid la margine, adică marginea lasă un anumit vârf F și intră în el, atunci o astfel de margine se numește o buclă (Figura 3.4).
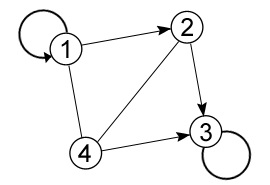
Figura 3.4 - Buclă ale graficului
Două sau mai multe grafice la prima vedere pot părea diferite în structura lor, care rezultă din imaginile lor diferite. Dar acest lucru nu este întotdeauna cazul. Luați două grafice (Figura 3.5). Ele sunt echivalente unul cu altul, deoarece fără a schimba structura unui grafic, se poate construi altul. Aceste grafice sunt considerate a fi izomorfe. adică posedând proprietatea că orice vârf cu un anumit număr de muchii într-un singur grafic are un vârf identic în celălalt.
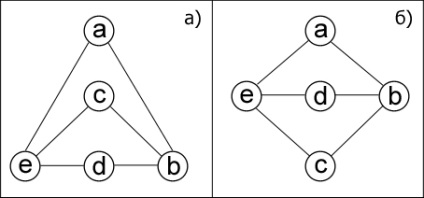
Figura 3.5 - Grafice izomorfe
Atunci când fiecare margine a graficului este asociată cu o anumită valoare, numită greutatea unei margini. atunci un astfel de grafic este ponderat. În diferite sarcini, diferite tipuri de măsurători pot acționa ca o greutate, de exemplu, lungimi, prețuri de rute etc. În reprezentarea grafică a unui grafic, valorile greutății sunt de obicei indicate în apropierea marginilor.
În oricare dintre graficele pe care le-am examinat, este posibil să se izoleze calea u, și nu doar una. O cale este o secvență de vârfuri, fiecare dintre ele fiind conectată la un vârf învecinat cu ajutorul unei muchii. Dacă coincide primul și ultimul punct, atunci o astfel de cale este numită ciclu. Lungimea căii este determinată de numărul de muchii care o compun. De exemplu, în figura 4.a, secvența [(e), (a), (b), (c)] servește. Această cale este un subgraf, deoarece definiția acesteia din urmă este aplicabilă, și anume: graficul G '= (V'. E ') este un subgraf al graficului G = (V.E), numai dacă V' și E 'aparțin lui V. E .
Un grafic, la fel ca majoritatea altor obiecte matematice, poate fi reprezentat pe un computer (stocat în memoria sa). Există mai multe modalități de a le interpreta, aici sunt cele mai faimoase dintre ele:
Folosind primele două metode implică stocarea graficului ca matrice bidimensională (matrice). Dimensiunile acestor tablouri depind de numărul de vârfuri și / sau de margini dintr-un anumit grafic. Deci dimensiunea matricei de adjuvant este n × n. unde n este numărul de vârfuri și matricele de incidență n × m. n este numărul de vârfuri, m este numărul de margini din grafic.