TEORIA ELEMENTARĂ DE ERORI
Erorile absolute și relative. Semnul de egalitate în calculele aproximative nu are același înțeles ca în algebra. Egalitatea nu înseamnă coincidența valorilor, ci doar apropierea valorilor. Precizia egalității aproximative, adică gradul de apropiere de valoarea exactă și gradul apropiat. caracterizează eroarea absolută.
În practică, în loc de o eroare absolută, care este de obicei necunoscută, utilizați eroarea absolută de limitare.
Cuvântul "limită" este omis pentru scurtă durată. Dacă sunteți interesat de corectitudinea calculului deja efectuat, atunci luați un număr care este probabil mai aproape de eroarea "adevărată". Ei numesc aceasta estimare de eroare. Estimarea erorii poate fi dură sau mai precisă. Eroarea poate fi specificată în prealabil, apoi calculul este efectuat astfel încât această inegalitate să fie satisfăcută.
Pentru a înregistra ceea ce este o valoare aproximativă cu eroare absolută. scrie:
Eroare relativă. deseori exprimată ca procent, este o cantitate astfel încât
Eroarea relativă caracterizează mai mult gradul de precizie al numărului aproximativ, deoarece este posibilă compararea preciziei specificării cantităților, ambele semnificativ diferite în ordine și exprimate în unități de măsură diferite.
Date fiabile și discutabile. Numărul inițial este numit adevărat în sens restrâns. dacă eroarea absolută a numărului nu depășește 1/2 din unitatea cifrei corespunzătoare acestei cifre.
Avem; de asemenea. Prin urmare, cifrele corecte în sens restrâns de 9 și 3. Numărul inițial este numit adevărat într-un sens larg. dacă eroarea absolută a numărului nu depășește unitatea cifrei corespunzătoare acestei cifre (în exemplele 9, 3 și 4). Cifrele din categoriile de ordine inferioară sunt chemative.
Secvența execuției de muncă
Exemplul 1. Sunt date valorile exacte și aproximative ale numărului. Găsiți erorile absolute și relative (soluția este prezentată în Figura 2.1)
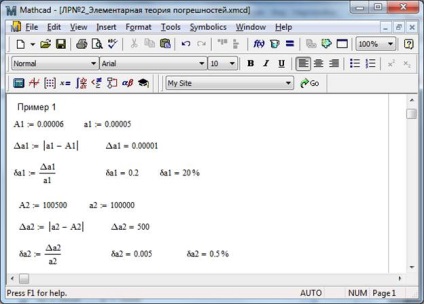
Fig. 2.1 - Soluția din Exemplul 1
Exemplul 2. Găsiți erorile limita absolute și relative ale numerelor și. dacă au doar numerele corecte: a) într-un sens restrâns, b) într-un sens larg.
Soluția sarcinii este prezentată în Fig. 2.2
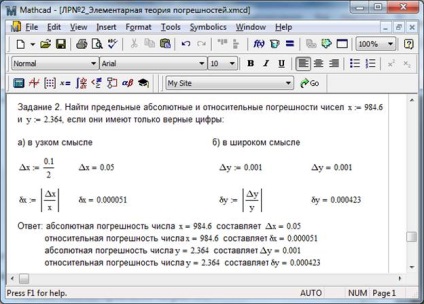
Fig. 2.2 - Soluția din exemplul 2
Exemplul 3. Având în vedere un număr și o eroare relativă. Determinați numărul de cifre corecte ale numărului prin eroarea sa relativă.
Soluție: deoarece și. atunci numărul are cel puțin două cifre, adevărat în sens restrâns. Definim eroarea absolută:
Prin urmare, într-un sens restrâns, numerele 2 și 3 sunt corecte.
Exemplul 4. Let. . Determinați numărul de cifre corecte într-un număr.
Soluție: deoarece și. atunci numărul are cel puțin o cifră care este adevărată în sens restrâns (figura 9). Să verificăm acest rezultat utilizând definiția unei figuri care este adevărată în sens restrâns.
Pentru aceasta, definim eroarea absolută:
Eroarea absolută rezultată nu depășește jumătate din unitatea sutelor. În consecință, figura 9 este adevărată într-un sens restrâns, atât în eroare relativă, cât și în eroare absolută.
Exemplul 5. Let. . Determinați toate cifrele corecte ale numărului.
Soluție: din moment ce. atunci numărul are cel puțin patru cifre care sunt adevărate în sens restrâns (numerele 2, 4, 3, 0). Noi calculam
Exemplul 6. La cântărirea a două încărcături s-au obținut următoarele valori ale masei lor kg și kg. Presupunând eroarea absolută de cântărire egală cu 1 g, determinați eroarea relativă în măsurarea masei corpurilor. Care corp este cântărit mai precis?
Soluția exemplului din Fig. 2.3.
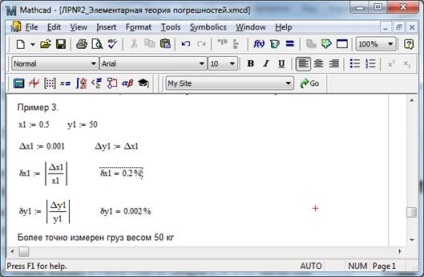
Fig. 2.3 - Soluția din exemplul 6
Exemplu 7. Determinați ce egalitate este mai exactă sau mai exactă
Soluție: găsiți valorile acestor expresii cu bócu atât este mai mare numărul de zecimale :. . Calculam erorile limita absolute, rotind-le cu exces:
Erorile relative limitative sunt:
Deci, cum. atunci ecuația este mai precisă.
Exemplul 8. Runda de cifre discutabile ale numărului, lăsând caracterele corecte:
a) în sens restrâns;
b) într-un sens larg.
Determinați eroarea absolută a rezultatului.
a) Lăsați. Conform condiției, eroarea; aceasta înseamnă că numerele 7, 2 și 3 sunt corecte în sens restrâns.Prin regulile de rotunjire, găsim valoarea aproximativă a numărului, păstrând zecimile:
Eroarea rezultată este mai mare de 0,05; prin urmare, este necesar să se reducă numărul de cifre într-un număr aproximativ de două:
Prin urmare, ambele cifre rămase sunt corecte în sens restrâns.
b); atunci. În acest număr, trei cifre sunt corecte într-un sens larg, așa că noi le rotunjim în jos, păstrând aceste trei cifre:
Prin urmare, într-un număr rotunjit, toate cele trei cifre sunt adevărate într-un sens larg.
Exemplul 9. Găsiți erorile limită absolute și relative ale numerelor dacă au numai cifrele corecte:
a) în sens restrâns;
b) în sens larg
Soluție: a) deoarece toate cele patru cifre sunt corecte în sens restrâns, atunci eroarea absolută. și eroarea relativă
b) deoarece toate cele cinci cifre ale numărului sunt adevărate într-un sens larg, atunci :;
Exemplul 10. Calculați și determinați erorile din rezultat.
4. Întrebări de testare:
1. Care sunt erorile absolute și relative?
2. Ce înseamnă cifra într-un sens larg și restrâns?
3. Cum se determină numărul de cifre corecte prin eroarea relativă a unui număr aproximativ?
4. Cum sunt determinate erorile absolute și relative în operațiile aritmetice?
Variante de sarcini pentru munca de laborator 2
1) Determinați ce egalitate este mai exactă.
2) Închideți cifrele îndoielnice ale numărului, lăsând semnele corecte:
a) în sens restrâns; b) într-un sens larg.
Determinați eroarea absolută a rezultatului.
3) Găsiți erorile limită absolute și relative
numere dacă au doar cifrele corecte:
a) în sens restrâns; b) într-un sens larg.
Variantele de sarcini sunt prezentate în tabelul. 1.1.