Modul de glisare este modul de funcționare al sistemului de relee, caracterizat prin mișcarea oscilantă a punctului reprezentativ de-a lungul liniei de comutare. Cu cât efectul derivatului este mai puternic în circuitul de reacție, cu atât liniile de comutare ale releului se rotesc în sens invers acelor de ceasornic. În același timp, intensitatea decăderii procesului tranzitoriu crește. În cazul în care o linie de schimbare unghi punct de comutare devine egal sau mai mic decât unghiul de înclinare al tangenta la traiectoria de fază a lungul căreia se deplasează reprezentative punct după comutarea releului, există condiții de existență a modului de alunecare [10].
Să considerăm apariția unui mod de alunecare în sistemul neliniar prezentat în Fig. 2.20, a, cu un releu ideal în absența acțiunii externe și pentru condițiile inițiale date x0 ¹ 0 și y0 = 0.
Lăsați starea inițială a punctului setat de sistem (x0. 0) (Fig. 2.25), din care reprezentantul deplasează punct de pe tipul de faza traiectoriei 1 înainte de întâlnirea cu linia de deplasare AB în punctul C. În acest moment, există un comutator releu, iar punctul de imagine se va deplasa de-a lungul fazei traiectoria până la punctul D. la punctul 2 al releului de tip D este comutat alt mod, atunci punctul de imagine se va deplasa de-a lungul traiectoriilor fazei 1. Imediat crește semnalul de feedback-ul rezultat va comuta releul și arătând Punctul se va deplasa de-a lungul traiectoriei de fază de tip 2 și așa mai departe, adică punctul reprezentând punctul de apropiere a acestui segment al liniei de comutare, alunecarea nu poate să o lase.
Astfel, punctul de imagine, ajungând la un punct D, trece în mod continuu de la calea spre calea de tip 1 de tip 2 și înapoi, așa cum au fost, alunecând de-a lungul liniei de comutare și se apropie asimptotic punctul de echilibru 0.
Așa cum se poate vedea din fig. 2.25, modul de alunecare este posibil pe secțiunile unde traiectoria de fază de tip 2 trece sub linia de comutare AB (după punctul D). Când poziția inițială a reprezentantului punctului (X02. 0) după tipul calea de sosire 1 într-un punct de pe linia de comutare D începe odată modul de alunecare. În cazul în care poziția inițială a punctului reprezentativ (x03. 0) modul de alunecare are loc după comutarea releului, atunci când diapozitivele reprezentative punct de pe linia de comutare AB în al patrulea cadranul. În acest din urmă caz, procesul tranzitoriu a depășit.

Fig. 2.25. Etapele traiectoriilor sistemului de relee
În acest exemplu, se presupune că comutarea releului are loc instantaneu, ca urmare, frecvența de comutare este infinit de mare și amplitudinea oscilațiilor este infinitezimală. Un astfel de mod de alunecare se numește limitare. Dacă luăm în considerare ambiguitatea caracteristicilor sau a benzii de interzicere, atunci comutarea releului în modul de alunecare are loc cu o frecvență finită, iar amplitudinea oscilațiilor diferă de zero.
În modul de alunecare limitativ, elementul releului poate fi înlocuit cu o legătură inerțială liniară echivalentă cu un coeficient de transmisie care tinde spre infinit (kp ® ¥). Apoi, funcția echivalentă de transfer a sistemului, corespunzătoare schemei structurale prezentate în Fig. 2.20, a, va fi
Prin urmare, pentru a limita sistemul glisant releu mod poate fi reprezentat printr-o schemă bloc echivalent de feedback integrator acoperit, sau pur și simplu ca un element de întârziere de ordinul întâi.
La sistemul de poziție x01 inițială (punctul M0 în Fig. 2.25) după comutarea releului M1, la punctul reprezentativ traiectoria lungul tipului faza 2 vine la origine, care caracterizează starea de repaus. În acest caz, procesul tranzitoriu va avea un timp minim, iar modul de funcționare al sistemului va fi optim în ceea ce privește viteza. Când doar un feedback de corecție a timpului de circuit constant astfel modul predeterminat Toc va exista pentru un anumit grup de valori inițiale atunci când punctul reprezentativ la momentul inițial este pe traiectoria 0 M0 M1. trecând prin origine; în toate celelalte cazuri, va exista un mod de alunecare fie imediat după comutarea releului, fie după mai multe operații de comutare.
Pentru ca procesul să fie optim ca răspuns la orice condiții inițiale, linia de comutare trebuie să fie traiectoria de fază care trece prin origine. O astfel de curbă a liniei de comutare indică o natură neliniară a acțiunii reacției corective. Linia de comutare nu se referă la traiectoriile de fază. Dar se poate face astfel încât să coincidă cu una dintre traiectoriile de fază. Apoi procesul în sistem va consta din două părți: o abordare a liniei de comutare pentru una dintre traiectoriile, alegerea cărora depinde de condițiile inițiale și deplasarea liniei de comutare în poziția de echilibru.
O reprezentare vizuală a setului de procese optime în diferite condiții inițiale este dată de portretul de fază prezentat în Fig. 2.26.

Fig. 2.26. Faza portret a sistemului optim pentru viteza:
AB - linia de comutare
La construirea sistemelor optime pentru viteză, sarcina principală este formarea unei funcții de control care caracterizează comutarea elementului releu. În Fig. 2.27 este o diagramă bloc a unui sistem cu feedback neliniar.
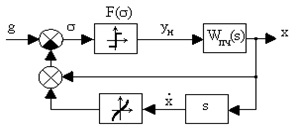
Fig. 2.27. Diagrama structurala a unui sistem optim pentru viteza
În general, sistemul care este optim în ceea ce privește viteza poate conține un dispozitiv de calcul care generează o funcție de feedback neliniare, elemente logice și o structură variabilă.