Luați în considerare echilibrul brațului și elaborați o diagramă de proiectare a forțelor care acționează asupra acestuia (figura 4). AB tija de rezervă în greutate. - G1 în T E, iar CD-ul de greutate baghetă. - G2 în t F. Punctele A și C se înlocuiesc cu suporturi fixe pivotabil reacții Xa, Xc, Ya și Yc.
Dacă luăm în considerare colțarul ca întreg, se transformă 4 necunoscutelor și ecuațiile de echilibru pentru sistemul plan arbitrar de forțe se poate face doar 3, deci este de două scheme de proiectare - pentru fiecare terminal separat (Figura 5), în timp ce există 2 mai multe reacții cunoscute în balama D.
Pentru fiecare schemă de calcul (figura 5), compunem trei ecuații de echilibru: două ecuații de forțe în proeminențe pe axele coordonatelor x și y, precum și suma momentelor de forțe raportate la m. D.


Ca rezultat, obținem un sistem de șase ecuații cu șase necunoscute.
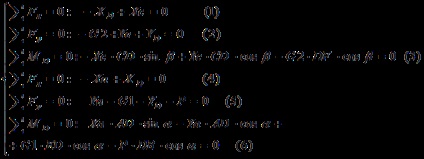
.
Substituim în ecuația (5) și exprimăm:
Din ecuațiile (1) și (4) găsim
.
Din ecuația (6) exprimăm Xa, de la (3) - Xc și echivalăm aceste expresii:
Noi substituim Ya și transformăm expresia:
exprimă și găsește Yc:
Pentru a găsi AD folosim teorema sinusoidală:
Când înlocuim valorile numerice, obținem Yc = 160 (H); Ya = 150 (H); Xc = Xa = 135 (H)
Verificați. Pentru a testa cea mai bună utilizare a tuturor schema de design consola (Figura 4) - Această schemă de calcul nu este în balama cuprinde reacțiile D. formează ecuația de echilibru sub forma sumei cuplurilor cu privire la orice punct (de exemplu, în raport cu punctul D) (Figura 4.) și verifică , că se transformă într-o identitate:
Într-adevăr, atunci când înlocuim valorile găsite, obținem identitatea.
Răspuns: Reacțiile Yc = 160 (H); Ya = 150 (H); Xc = Xa = 135 (H).
Calculele calculatorului:
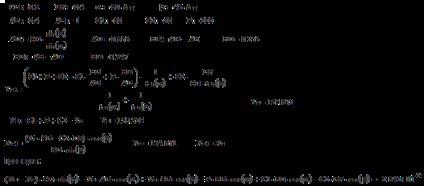
Rezolvăm această problemă în mediul Mathcad folosind metoda iterativă:

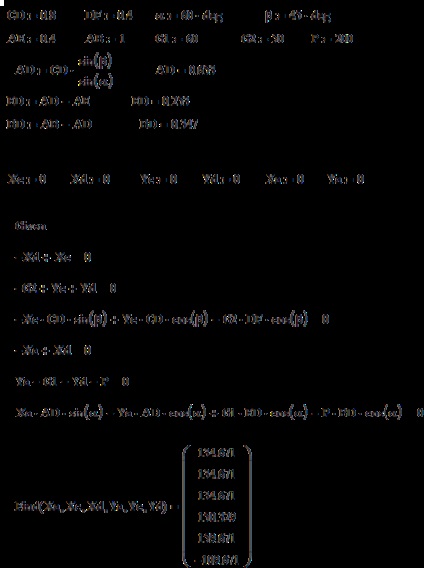
Exemplu SP-5. Echilibrul sistemului forței spațiale (Meshchersky, 8.24)
greutate Omogen cadru dreptunghiular 200 atașat la perete H prin intermediul unei articulații sferice A și bucla B, și a avut loc într-o frânghie poziție CE orizontală legată de cadrul și punctul C la E unghii înfipt în perete, la aceeași linie verticală A, și
. Determinați tensiunea cordonului și reacțiile de susținere.
Având în vedere valorile numerice, obținem T = 200 H, XA = 86,6 H, YA = 150 H, ZA = 100 H, XB = ZB = 0.
Verificați. Pentru a verifica, vom compune încă trei ecuații de echilibru sub forma proiecțiilor forțelor pe axa x1. y, z1 (Figura 6) și verificați dacă devine o identitate:
Într-adevăr, atunci când înlocuim valorile găsite, obținem
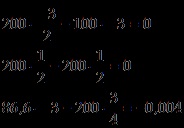
Răspuns. Forța de întindere este T = 200 N, reacțiile de referință XA = 86,6 N, YA = 150 N, ZA = 100 N, XB = YB = 0.
O soluție de calculator. Pentru a rezolva un sistem de ecuații liniare, se poate folosi, de exemplu, metoda matricei. Ecuațiile de echilibru (1), (2) și (3) vor fi scrise în formă standard, ținând necunoscuți în partea stângă a ecuațiilor:
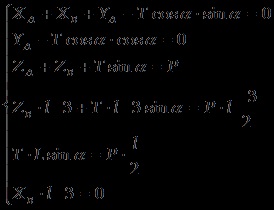
Soluția de matrice are forma:
