Primele șosele și căile ferate aveau aspectul secțiunilor rectilinii conectate prin arce de cercuri. Dar când autovehiculele și trenurile au început să se deplaseze la viteze mai mari, o apăsare incomodă și periculoasă a apărut la intrarea în secțiunile curbe. Inginerii au început să caute o soluție la problemă și au găsit-o în matematică și fizică. Vrei o explicație simplă, de ce este clotatul folosit ca curbă de tranziție?
Imaginați-vă că trebuie să proiectați o autostradă sau un tren de mare viteză. Desigur, veți încerca să o faceți cât mai direct posibil, dar vor apărea și câteva secțiuni curbiliniere. Deoarece cea mai simplă curbă a tuturor este un cerc, este mai ușor să conectați secțiuni drepte între ele prin arce de cercuri. Ceva ca o bandă transportoare.
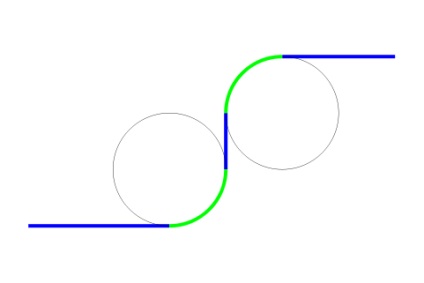
Se pare că astfel au fost primele proiecte și, din moment ce primele mașini și trenuri nu s-au mișcat prea repede, totul a mers fără probleme. Dar lucrurile s-au schimbat atunci când vehiculele puteau atinge viteze mai mari. La intrarea în secțiunile curbiliniare, la intersecțiile dintre secțiuni, apărea o împingere bruscă. O afacere rea.
Așa că inginerii au început să studieze ce sa întâmplat, și cum ar putea fi remediată aceasta. Răspunsul este simplu de înțeles și necesită cunoașterea a numai două lucruri. Primul vine din geometrie - este raza de curbură, conceptul este destul de intuitiv.
Pentru un cerc, raza de curbură este doar raza cercului. Pentru o linie dreaptă, putem presupune că acesta este un cerc foarte mare, un cerc de rază infinită. Astfel, raza de curbură a liniei va fi infinită. Ușor, nu-i așa?
Al doilea concept al fizicii este o forță centrifugă, care este și mai intuitivă, deși esența acestui concept este mult mai complicată decât pare.
Cu siguranță știți că forța - o „accelerare ori masa«»și simplificând un pic, forța centrifugă este de forma (nu vă faceți griji, merge pe o formulă, dar este unic, și este simplu):
unde - masa, - viteza și - prietenul nostru, raza de curbură.
Pe de o parte, avem masa și viteza, care se înmulțesc în această formulă. Astfel, cu cât sunt mai mari, cu atât este mai mare forța centrifugală. Acest lucru este de înțeles: dacă vă mișcați mai repede, forța centrifugă va fi mai mare și va fi mai mare dacă masa dumneavoastră este mai mare.
Pe de altă parte, avem o rază de curbură, care stă în numitor. Astfel, prin creșterea razei, este posibilă reducerea forței centrifuge. Este clar: raza de curbură este linie dreaptă infinită, astfel încât ( „la infinit prin divizarea«») în timpul conducerii forța centrifugă dreaptă este egală cu zero. De asemenea, știți că atunci când conduceți cu aceeași viteză forța centrifugă este mai mică decât pe o «» curbă (cu o rază mai mare) decât celelalte «mai„deschise»„curba mai închisă (cu o rază mai mică).
Ce pot face? Să ne uităm la formula. Avem
masă, la care ne multiplicăm. Pentru ao reduce, trebuie să reduceți masa mașinii / trenului și a pasagerilor ... știi bine că nu este atât de simplu de făcut.
Viteza la care se înmulțește (și mai mult în pătrat). Puteți merge mai lent, dar atunci va dura mai mult timp ... și, desigur, este puțin probabil ca cineva să-i placă.
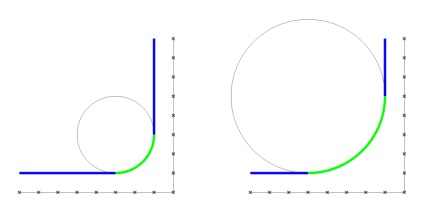
Raza de curbură, la care ne împărțim. Pentru o linie, este infinită, nu o poți schimba. Da, puteți crește raza cercului, dar apoi (ca în imaginea de mai sus) segmentele liniilor drepte vor deveni mai scurte ... și cu siguranță nu sunt ca oricine.
Deci, trebuie să vă gândiți la o altă posibilitate. Puteți să ghiciți care dintre ele?
Desigur, puteți introduce o curbă de tranziție între linie și cerc. De asemenea, ar fi frumos ca, în această tranziție, raza de curbură să scadă ușor de la infinit (sau de la un număr mare) pentru o linie dreaptă la raza cercului.
Conform formulei, forța centrifugă se va schimba apoi ușor, mai degrabă decât brusc.
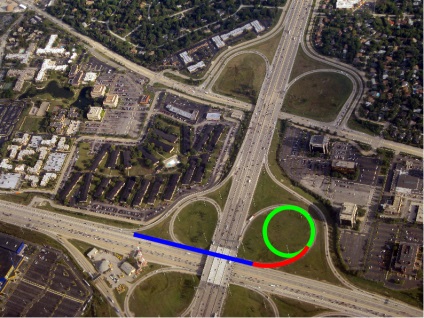
Deci, doriți ca raza de curbură să scadă pe măsură ce crește distanța? Stai puțin. Există două valori ... Vreau ca unul să devină mai mic în timp ce celălalt devine mai mare ... Aceasta este ceea ce în școală se numește invers proporțional!
Adică, doriți ca raza de curbură și cărarea parcursă să fie invers proporțională. și
Ce înseamnă asta? Da, asta înseamnă că munca lor este întotdeauna același număr.
Această proprietate determină curba clotului, cunoscută de matematicieni și fizicieni. Ecuația sa are forma, (unde este constanta, care este luată în pătrat pentru a facilita construirea curbei).
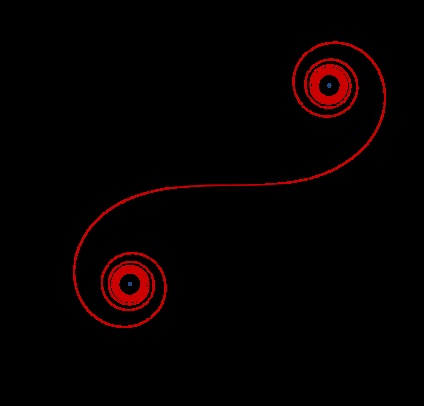
Deci, când mergeți pe șosea și pe calea ferată, vă deplasați, de regulă, într-o linie dreaptă - un clotaj - un cerc - un clotoid - o linie dreaptă. Astfel, forța centrifugă variază treptat, iar tu poți transforma treptat în loc să o faci brusc.
Data viitoare la colțuri amintiți-vă că matematica și fizica vă ajută
Tot ceea ce este menționat mai sus, se referă și la trecerea de la orice curbă la o altă curbă.
Pe lângă căile ferate și drumurile mai mult sau mai puțin convenționale, clotatul este utilizat și pe traseele de curse și pe coaster.

Aparent, primul studiu a început clotoidă matematician elvețian Jacob Bernoulli în 1694, în contextul problemei teoriei elasticității. Această problemă a fost rezolvată în 1744 de către matematicianul și fizicianul Leonard Euler, care a dat o caracterizare a curbei. În jurul 1818, fizicianul francez Augustin-Jean Fresnel redescoperit clotoidă studiind difracției luminii, și cu ajutorul integralelor primit parametrizare a curbei, parametrizarea echivalentă Euler. În 1874, fizicianul francez Marie Alfred Cornuus a folosit această expresie pentru a construi cu exactitate curba. Mai târziu, în 1890, inginerul american Arthur Talbot, redescoperă din nou clotatul în căutarea unei curbe de tranziție pentru căile ferate. Dacă doriți să aflați mai multe despre istoria clotoidelor, puteți citi articolul Spirală Euler: o istorie matematică. scris de Raph Levien.
Astfel, clotoidul este cunoscut și ca spirala Cornu sau spirala Euler. Deși curba clotoidă a fost mai bine cu examinarea proprietăților au fost luate în considerare alte curbe de tranziție posibile, cum ar fi Bernoulli lemniscate și Cassini oval (vezi de exemplu aici :. Algunas notas las curvas sobre de las carreteras 1929.).