În practică, avem de-a face în mod constant cu valori aproximative, ecuatii, formule construi pe punctele comploturi, elimina rădăcinile numerelor, rezolvarea ecuațiilor, etc. In teorie, calcule aproximative, care în prezent este în curs de dezvoltare rapid, sunt metode deosebit de relevante utile .. pentru rezolvarea unei mari categorii de probleme matematice. Să vorbim despre câteva dintre aceste metode.
Calculul circumferinței unui cerc utilizând formulele de dublare este un exemplu concret al unui algoritm pentru obținerea valorilor aproximative ale π. Această metodă este interesantă din punct de vedere istoric, deoarece, probabil, aceasta este una dintre cele mai vechi metode de calculare aproximative. Formula de dublare conectează lungimile laturilor a și a2n ale regulilor n- și 2n-gons înscrise într-un cerc (diametrul este egal cu 1):
și permite, pornind de la un hexagon regulat, a cărui lungime este egală cu 1/2, pentru a calcula succesiv a12. A24. A48. ..., până ajungem la valoarea perimetrului, care corespunde unei precizii date de calcule. Se poate demonstra acest lucru
π - nan <6/n 2. n ≥ 3.
Această inegalitate ne permite nu numai să stabilim faptul că procesul converge (adică, π - nan → 0 ca n → ∞), dar și să planifice calculele în avans. Deci, dacă trebuie să asigurăm corectitudinea calculelor, egală cu 10 -3. atunci este suficient să se ia n astfel încât inegalitatea 6 / n 2 <10 −3. т. е. n> √6000 sau n ≥ 78> √6000.
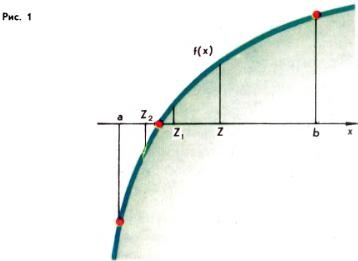
Metoda furcii utilizată pentru a găsi rădăcinile ecuației f (x) = 0 pentru funcțiile continue f este destul de generală. Fie f definit și continuu pe intervalul [a, b], are o rădăcină unică și f (a) <0, f(b)> 0. Luați în considerare valoarea f (z), unde z = (a + b) / 2 este punctul de mijloc al intervalului [a, b]. Dacă f (z) = 0, atunci z este rădăcina dorită. Dacă f (z) ≠ 0, atunci cele două segmente [a, z] și [z, b] va selecta una pentru care valoarea funcției f la capete au semne diferite (în Fig. 1 este un segment [a, z] ), și o desemnează cu [a1. b1] astfel f (a1) <0 и f(b1 )> 0. Dacă luăm acum un punct z1 = (a1 + b1) / 2, apoi, din nou, sau f (z1) = 0 sau f (z1) ≠ 0. În al doilea caz a două segmente [a1. z1] și [z1. b1], selectați cel la căruțe funcția f preia valori ale diferitelor semne (în figura 1, [a2. b2] = [a, z1]). Dacă vom continua acest proces, fie se va rupe la un pas, fie vom obține o secvență de segmente imbricate [a, b], [a1. b1] [a2. b2], ..., pentru care un ≤ an + 1
În plus, avem inegalitățile:
care vă permit să planificați calculele cu o precizie dată.
Utilizarea derivatului în studiul comportamentului funcției face posibilă obținerea multor formule utile pentru calcularea aproximativă a valorilor funcțiilor. Din definiția derivatului rezultă că pentru creșterile mici Δx ale argumentului x0 pentru funcția f se poate scrie o egalitate aproximativă
Geometric, acest lucru înseamnă că, în apropierea punctului x = x0 ne Graful (x) graficul y = f înlocuit cu o tangentă la graficul y = f (x) la punctul cu abscisa x = x0 (Fig. 2).
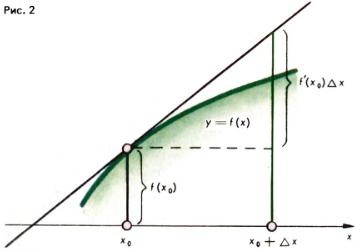
Astfel, se obțin, de exemplu, formule aproximative (eficiente pentru Δx mici):
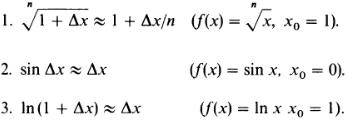
Metoda tangentelor Newton pentru soluția aproximativă a ecuațiilor f (x) = 0 constă în următoarele. Să presupunem că funcția f are o rădăcină unică c în intervalul] a, b [și este diferențiabil la fiecare punct al intervalului] a, b [și f '≠ 0 în acest interval. Luăm un punct arbitrar x0 ∈] a, b [și scriem ecuația tangentă la graficul funcției f la un punct cu abscisa x = x0.
Graficele f (x) și tangenta sa sunt apropiate una de alta pentru micile x - x0. și, prin urmare, este normal să se aștepte ca punctul x1 al intersecției curbei tangente cu axa abscisă să fie localizat lângă rădăcina c (figura 2). Avem:
Continuând acest proces, obținem o secvență (xn) de puncte definite prin formula
Se știe că inegalitatea
unde A> 0 este o constantă care nu depinde de n. Această inegalitate arată că, chiar și pentru n suficient de mică, se obține o precizie suficient de mare a aproximațiilor.
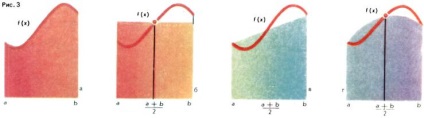
Un calcul aproximativ al zonelor (integrale) ale trapezoidelor curviliniare (figura 3a) se bazează pe considerente geometrice simple. Dacă intervalul [a, b], a Dacă înlocuim graficul funcției pe intervalul [a, b] nu este segmentul de linie, iar graficul parabolei (fig. 3 g) ca aproximare pentru S lua o zonă trapez curbiliniu delimitată de arcul parabolei, obținem formula Calculul integrat face posibilă calcularea cu mai multă precizie a zonei trapezului curbilinii.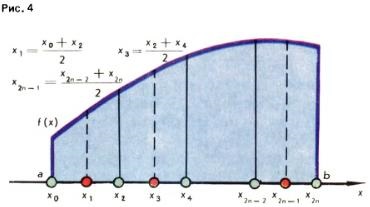
Pentru a realiza cea mai mică eroare posibilă cu calcule aproximative ale lui S, intervalul de la a la b este împărțit în 2n părți egale. Apoi, arcul graficului y = f (x) este împărțit în n părți (Figura 4). Dacă acum folosim metodele de aproximare anterioare pentru fiecare dintre aceste arce mici, atunci pentru zona S obținem valori aproximative sub forma sumelor zonelor n trapezoidale curbilinii; avem:
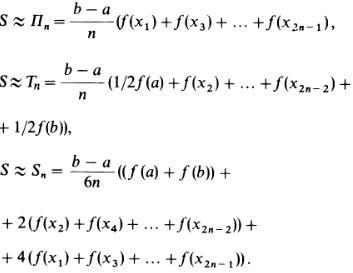
Primele două formule poartă numele formulei de dreptunghiuri și formulele trapezoidelor, iar cea din urmă formulele lui Simpson, numite după matematicianul englez T. Simpson (1710-1761).
Estimările erorii în aceste formule aproximative sunt practic calculate după cum urmează. număr n selectat, un multiplu de 4, și S se bazează pe formula Simpson (mai exactă a celor trei) numărul punctelor n și n / 2 (Sn și Sn / 2) și este de aproximativ determinat folosind raportul de eroare de calcul