Un număr numit limita funcției y = f (x) x tinde la infinit, dacă este cazul, chiar arbitrar mic număr pozitiv e, există un număr întreg pozitiv S (independent de e, adică, S = S (e) ) că pentru toate x astfel încât | x |> s, inegalitatea: | f (x) - A | Rețineți că diferența dintre această definiție și definiția limitei unei secvențe este aceea că pentru o secvență variabila n ia doar valori naturale și aici x ia orice valoare. Limita unei funcții la infinit este notată de sau Înțelesul definiției este că pentru valori suficient de mari ale argumentului, valorile funcției arbitrar diferă puțin de numărul A în valoare absolută. Sensul geometric al definiției poate fi explicat în figura 2.3. Figura 2.3 - Semnificația geometrică a limitei unei funcții la infinit
f (x) A A pentru x ¥ ..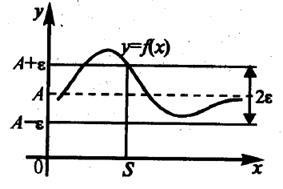
Astfel, numărul A este limita funcției y = f (x) când x ® ¥, dacă pentru orice e> 0 există un număr S> 0 astfel încât pentru toți x astfel încât | x |> S, ordonatelor corespunzătoare graficului f ( x) va fi inclus în e-vecinătatea punctului A pe axa de coordonate. În acest caz, partea corespunzătoare a graficului va fi într-o bandă 2e largă.
Noțiunea de limită a unei funcții la infinit poate fi de asemenea formulată ca o tendință de infinitate a unui semn clar. Diferența va fi că argumentul funcției tinde la infinit magnitudine absolută și x ® + ¥ (apoi în definiția în loc de | x |> S va fi inegalitatea x> S) sau x ® - ¥ (apoi în definiția în loc de | x > Va exista o inegalitate x <-S).
Limita unei funcții la un punct
Un număr numit limita funcției y = f (x) cu x tinde la x0 (sau x0 vtochke), dacă este cazul, chiar arbitrar mic pozitiv număr e, există un număr d pozitiv (independent de e, adică d = d (e)) astfel încât pentru toate x x x0 astfel încât | x - x0 | Limita unei funcții la punctul x0 este notată cu sau Înțelesul definiției este că pentru toate valorile argumentului suficient de apropiate de x0. valorile funcției diferă arbitrar de numărul A în valoare absolută. Sensul geometric al definiției poate fi explicat în figura 2.4.
f (x) ® A pentru x ® x0.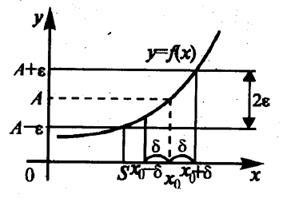
Figura 2.4 - Semnificația geometrică a limitei unei funcții la un punct
Astfel, numărul A este limita funcției y = f (x) pentru x ® x0. dacă pentru orice e> 0 există un d-cartier de x0. că pentru toate x x x0 din acest cartier ordonatele corespunzătoare ale graficului funcției f (x) vor fi cuprinse în e-vecinătatea punctului A pe axa de coordonate. În acest caz, partea corespunzătoare a graficului va fi într-o bandă 2e largă.
Subliniem că definirea unei limite nu presupune existența unei funcții la punctul x0 însuși. Având în vedere limita, se presupune că x tinde la x0. dar nu atinge această valoare. Prin urmare, prezența sau absența unei limite este determinată de comportamentul funcției într-o vecinătate a punctului x0. dar nu prin faptul că o funcție este definită la punctul în sine.
Conceptul limitei unei funcții la un punct poate fi formulat și în sensul unei limite unilaterale. Diferența va fi că argumentul funcției ia doar valorile x În cazul în care. atunci. și invers (adică, în cazul în care, la o anumită funcție punct are limite pe stânga și din dreapta, acestea sunt egale, cu două sensuri limita, de asemenea, există și este egal cu același număr, și din contra - în cazul în care există o limită bilaterală, există o singură față, este egală cu ). Condiția care determină comportamentul argumentului, pe care am notat-o sub notația unei limite, va fi numită baza limitei și notată cu nota B.Articole similare