Fie n = 2m - un număr chiar și yi = f (xi) (i = 0..n) - valoarea funcției y = f (x) pentru puncte echidistante a = x0. x1. x2. ..., xn = b cu pasul h = (b-a) / n = (b-a) / 2m. O pereche de secțiuni (Fig.3) curba y = f (x) se înlocuiește cu parabolei y = L (x), ale căror coeficienți sunt alese astfel încât să treacă prin punctul y0. y1. v2.
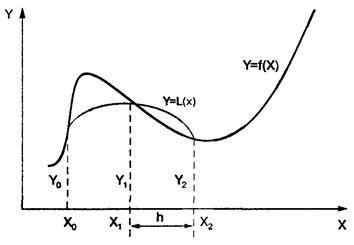
Fig.3 Interpretarea geometrică a integrării prin metoda Simpson.
Zona trapezoidului curbilinar, delimitată mai sus de o parabolă, este:
Rezumând zonele tuturor trapezoidelor curvilineare, obținem:
În cazul în care p = 6-p, p = 4. Prin urmare, formula Simpson pentru integrarea numerică are forma:
Restul termenului are forma:
În practică, pentru a evalua eroarea absolută a formulei Simpson, se folosesc următoarele relații:
În acest caz, de regulă, obține pentru o supraevaluare.
2. Rule Runge (n - even) oferă o evaluare mai subtilă:
Dar, în același timp, se poate dovedi a fi o estimare scăzută, care ar trebui să fie temută.
Formulele pentru dreptunghiuri și trapezuri dau valoarea exactă a integrului atunci când integrarea f (x) este liniară. pentru atunci f "(x) = 0, iar formula Simpson este exactă pentru polinomiale până la a treia putere. deoarece în acest caz f (4) = 0.
Dacă funcția y = f (x) este dată în tabele și derivații săi sunt greu de găsit, în ipoteza lipsei componentelor oscilante rapide pot fi utilizate formule aproximative pentru erori, exprimate în termeni de diferențe finite:
1. Să fie necesar să se calculeze integral cu precizie # 949;. Folosind formula corespunzătoare termenului R, alegeți h astfel încât inegalitatea să fie satisfăcută.
2. Numărătoarea dublă. (Rule Runge).
SOLUȚIA NUMERICĂ A EQUACAȚIILOR TRANSCENDENTE ȘI NONLINEARE.
Dacă ecuația algebrică sau transcendentală este destul de complexă, rădăcinile acesteia sunt relativ rareori găsite cu exactitate. Prin urmare, o mare importanță este obținută în metodele de aproximare a rădăcinilor ecuației și estimarea gradului de precizie a acestora.
Procesul de a găsi valori aproximative ale rădăcinilor ecuației:
unde funcția f (x) este definită și continuă în unele finite sau
intervalul infinit a
Orice înțeles # 955;, inversând funcția f (x) la zero, adică astfel încât f (# 955;) .. = 0 se numește rădăcina ecuației (1) sau zero, funcția f (x).
Separarea rădăcinilor înseamnă divizarea întregului interval de valori permise în segmente, fiecare conținând o rădăcină. Separarea rădăcinilor se poate face în două moduri - grafic și analitice.
Metoda grafică de separare a rădăcinilor. a) reprezentată grafic funcție y = f (x) pentru ecuația forma f (x) = 0. Valorile rădăcinilor reale ale ecuațiilor sunt generate absciselor punctelor de intersecție ale funcției y = f (x) cu axa x (figura 1);
b) reprezintă ecuația (1) sub formă (X) = g (x) și construiți graficele funcțiilor
y = (X) și y = g (x). Valorile rădăcinilor reale ale ecuației sunt abscise ale punctelor de intersecție ale grafurilor funcțiilor y = (X) și y = g (x) (figura 2).
Segmentele, în care este închisă o singură rădăcină, sunt ușor de găsit.
Metoda analitică pentru separarea rădăcinilor se bazează pe următoarea teoremă:
Dacă o funcție continuă pe un segment are valori de semne diferite la capetele unui segment, adică, . există cel puțin o rădăcină a ecuației din interiorul acestui segment; dacă în acest caz
derivatul păstrează semnul în interiorul intervalului. atunci rădăcina este unică.
Specificarea rădăcinilor la o anumită precizie.
Adică îngustarea segmentului de localizare a rădăcinilor [a, b]. Să luăm în considerare mai multe metode.
Metodă de divizare pe jumătate (dihotomie).
Rădăcina trebuie să fie separată și să aparțină segmentului. Gasim mijlocul segmentului dupa formula (figura 3). În cazul în care. atunci c este rădăcina dorită.
În cazul în care. apoi ca un nou segment de izolare a rădăcinilor vom selecta jumătate sau. la sfârșitul căruia ia valori de semne diferite. Cu alte cuvinte, dacă. atunci rădăcina aparține segmentului. dacă - un segment. Segmentul rezultat este împărțit din nou la jumătate, aflăm.
Calculăm. alegeți segmentul etc. Imediat ce sa terminat. apoi ca valoare aproximativă a rădăcinii, calculată cu precizie. pot primi.
După fiecare repetare, segmentul pe care se află rădăcina este înjumătățit, adică după n iterații se reduce cu 2 n ori. Astfel, numărul de iterații n din această metodă depinde de precizia predefinită # 949; și pe lungimea segmentului original și nu depinde de forma funcției f (x). Acesta este un avantaj important al metodei de divizare în comparație cu alte metode. Metoda, totuși, converge lent când se stabilește o precizie ridicată a calculului.
Lăsați intervalul [a, b] funcția f (x) este continuă și preia capetele valorilor segmentului de diferite semne și derivați ai f „(x) și f„(x) să mențină un semn constant pe intervalul (a, b). Apoi, există patru cazuri de curba locația arcului (Figura 4).
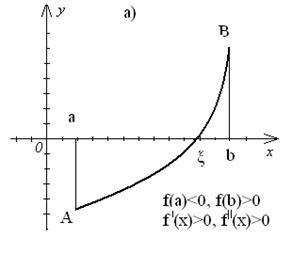
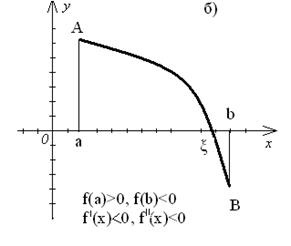
Metoda de coardele pentru aproximarea următoare să ia punctul de intersecție cu axa X a liniei (Figura 5) care leagă un punct (a, f (a)) și (b, f (b))
Și unul dintre aceste puncte este fix - unul pentru care semnele f (x) și f "(x) sunt aceleași.
Pentru figura 5, capătul fix al coardei este x = a.
Ecuația coardă AB:
Punctul de intersecție al coardei cu axa X (y = 0) :.
Acum rădăcina este pe [a, c1]. Înlocuim b cu c1.
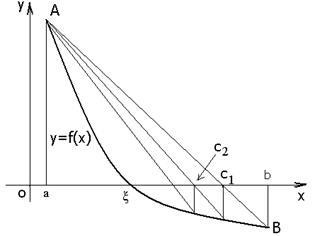
Figura 5. Ilustrație a metodei acordurilor.
Aplicând metoda chordului în acest segment, obținem:
Să continuăm, etc. obținem: (2) Condiția pentru finalizarea calculelor:
Pentru a estima eroarea, se poate folosi formula generală:
Astfel, dacă f (x) # 8729; f "(x)> 0, valoarea aproximativă a rădăcinii este găsită prin formula (2), în cazul în care f„(x) # 8729; f"(x) <0 (т.е. фиксируется х = b), то по формуле: