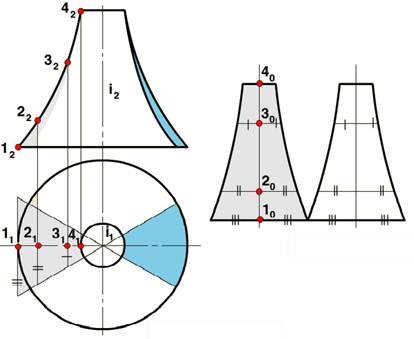
Când se construiește o maturare a suprafeței de revoluție, ea este împărțită prin intermediul meridianelor în părți relativ înguste și egale. Fiecare astfel de fracțiune este aproximată de o suprafață cilindrică care atinge suprafața dată în punctul meridianului mediu de distanță. Acest meridian mediu este secțiunea normală a unei suprafețe cilindrice. Limitele suprafeței cilindrice vor fi planurile meridianelor, care limitează fracțiunea considerată (figura 5). Suprafața rotației poate fi ruptă în paralelă prin fracții și în jurul fiecărui lob care descrie un con trunchiat de rotație. Apoi, construiți o maturare a fiecărei acțiuni.
Cea mai mare aplicație a suprafețelor desfășurate se află în sferă. În practica de inginerie, este adesea folosit pentru că are o suprafață minimă și cel mai mare volum în comparație cu alte suprafețe care au aceeași suprafață.
Există mai multe moduri de a construi măturări ale suprafeței unei sfere, toate oferind soluții aproximative cu o anumită precizie.
Cea mai obișnuită metodă este aceea că suprafața sferei este împărțită de meridiane în părți (de exemplu, 12 părți). O parte a sferei închise între două secțiuni adiacente este aproximată de un cilindru, cel mai adesea descris. Partea este îndreptată, combinată cu planul și se obține o "petală", lungimea căreia este egală cu jumătate din circumferința secțiunii mai mari a sferei, iar lățimea este egală cu 1/2 din lungimea acestui cerc. Douăsprezece astfel de petale constituie o curățare completă a suprafeței mingii. Nu toate petalele sunt prezentate în figură (figura 6). Construcția petalelor se realizează după cum urmează: pe o linie dreaptă arbitrară, lungimea ecuatorului este așezată și împărțită în 12 părți. În mijlocul fiecărei părți, sunt trase linii drepte perpendiculare pe desfășurarea ecuatorului și segmente de segmente și segmente egale cu 1/4 din lungimea meridianului (ecuator). Apoi părțile superioare și inferioare sunt împărțite în trei părți și prin punctele de divizare conduc segmente egale cu lungimea arcurilor situate între secțiunile meridionale de pe paralelele corespunzătoare. Prin conectarea punctelor obținute în funcție de model, se obține o contur complet al fiecărui lob.
Când desenați puncte pe o maturare, se folosesc paralele care trec prin punctele de divizare a meridianului. De exemplu, punctul N este pe marginea primei și a celei de-a doua petale.
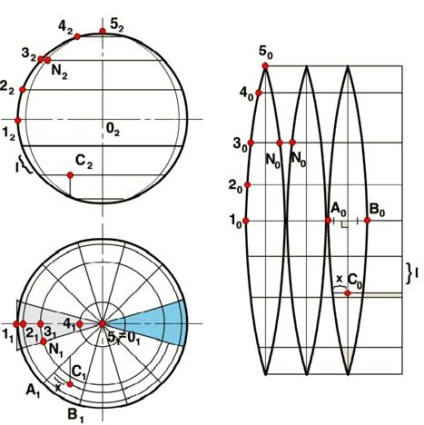
Punctul C este în partea de jos a celei de-a treia petale; pentru ao construi pe o scanare, este necesar să tragem prin punctul paralel și să stabilim distanța față de cea mai apropiată paralelă, măsurată de-a lungul meridianului principal l, pe perpendicularul prin mijlocul lui A0B0. Apoi, executați o scanare paralelă și aplicați o distanță x măsurată de la cel mai apropiat meridian la proiecția orizontală.
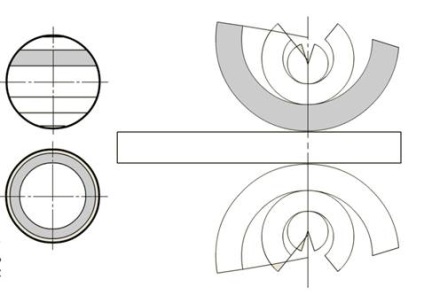
Suprafața este ruptă de paralele cu curelele. Suprafața sferei este aproximată prin conuri de torsiune inscripționat sau descrise, susținute de o paralelă. Problema este redusă la construirea unei serii de suprafețe conice pentru o singură curățare a secțiunii medii cilindrice, unde ecuatorul este secțiunea normală a cilindrului.