Atunci când însumarea erorilor este ghidată de următoarele:
1. Erorile sistematice -

2. Erori aleatorii, se adaugă evaluarea lor RMS la baza corelațiilor lor reciproce, bazată pe dependența cunoscută a teoriei probabilității
(1.44) unde
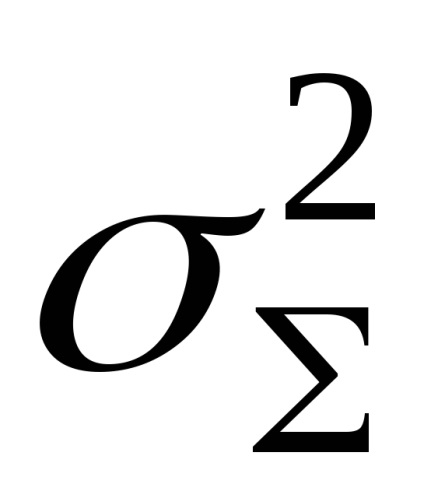
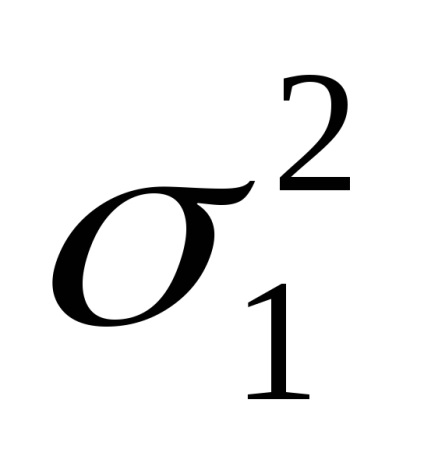
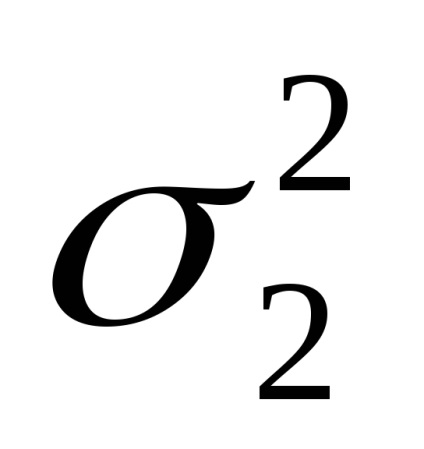
Eroare medie pătrată medie totală
De obicei, nu există informații privind măsura de corelare, deci în practică sunt considerate două cazuri extreme: r = 0, r = ± 1. Dacă r = 0, erorile aleatorii sunt independente din punct de vedere statistic (ne-corelate), iar erorile sunt sumate geometric:
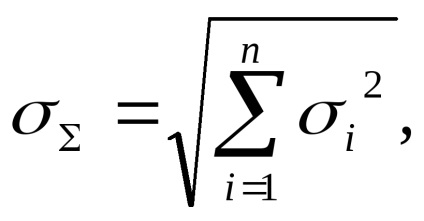
unde

Dacă erorile aleatorii sunt puternic corelate (r = ± 1), atunci există o relație funcțională între rezultatele măsurătorilor. În acest caz, se adaugă dacă r = + 1,
sau scade dacă r = -1
Sumarea unei erori sistematice cu o eroare aleatorie se realizează luând în considerare relațiile de corelație conform aceluiași principiu ca și sumarea erorilor aleatorii.
I.I3. Erori ale măsurărilor indirecte
Pentru măsurările indirecte, valoarea cantității fizice căutate se găsește prin măsurători coordonate ale altor cantități asociate cu cantitatea măsurată printr-o dependență funcțională cunoscută. Aceste alte cantități vor fi numite argumente măsurabile. Valorile argumentelor se găsesc cel mai adesea ca urmare a măsurătorilor directe, dar uneori ca rezultat al măsurărilor comune, cumulate sau indirecte. Prin urmare, apare problema: pentru a determina eroarea funcției pentru erorile date în argumente.
Valoarea măsurată a lui Q este legată de argumentele măsurate de dependență
Există cazuri de relație implicită între Q și Qi.
Prin tipul dependenței funcționale, măsurătorile indirecte se disting printr-o relație liniară între cantitatea măsurată și argumentele
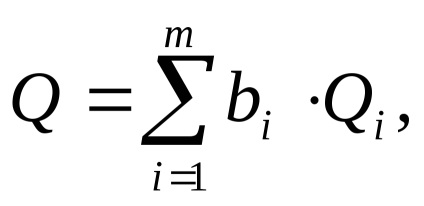
cu dependență neliniară
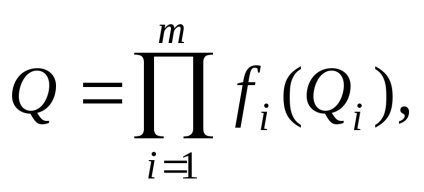
cu o dependență de tip mixt
Acum estimăm rezultatul
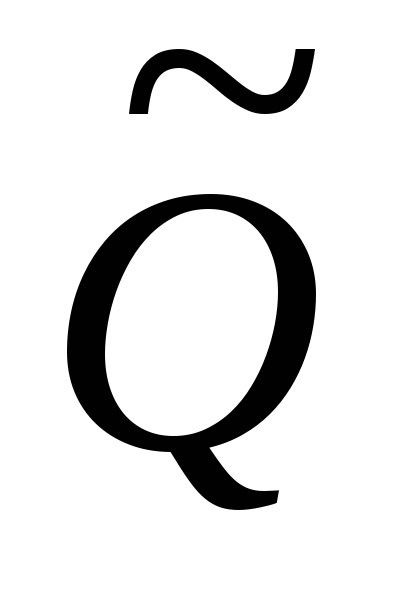
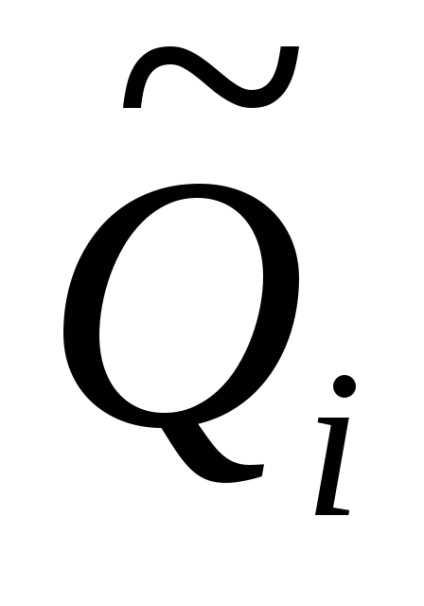
Fiecare argumente Qi să fie caracterizate de o estimare
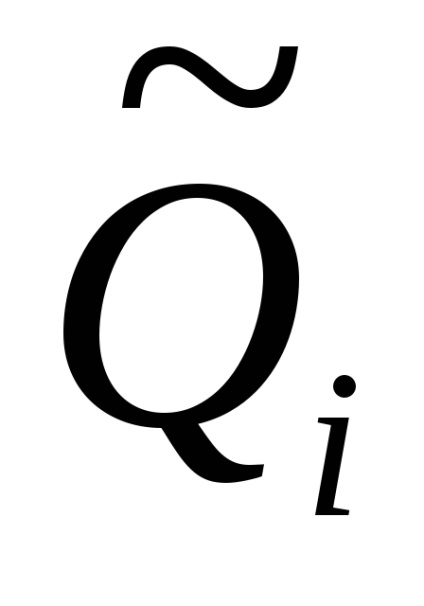
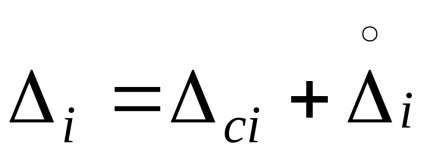
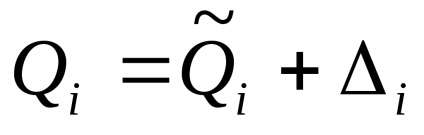
Din (1.49) obținem o estimare a rezultatului
și erorile de măsurare indirectă
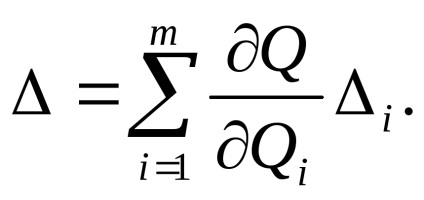
Admisibilitatea unei astfel de evaluări trebuie verificată. derivați de
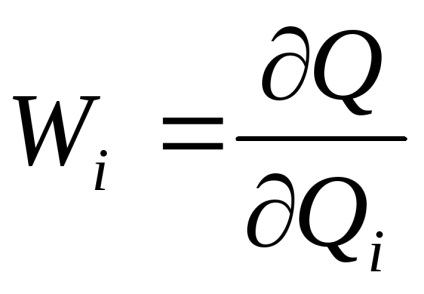
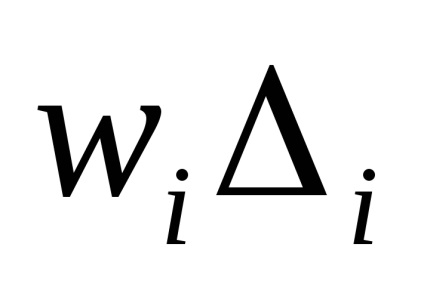
Luați în considerare erorile aleatorii. Mai mult, se presupune că componentele sistematice ale erorilor din estimările tuturor Qi sunt constante. Să exprimam o estimare a unei valori medii quadratice a unei erori aleatorii a rezultatului intenției indirecte ca
unde
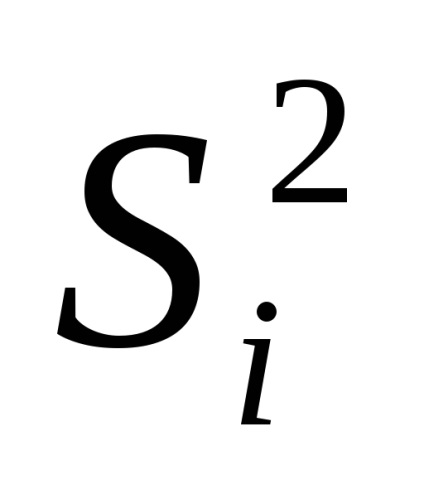
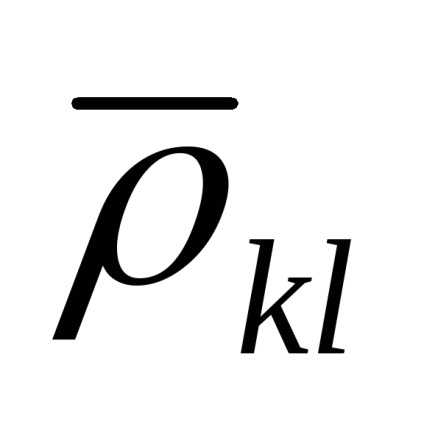
Atunci când dimensiunile argumentelor nu se fac simultan prin mijloace diferite de măsurare, coeficientul de corelare este aproape de zero și
Noua notație introdusă pentru estimarea medie pătrată evidențiază faptul că variațiile rezultatelor observării sunt utilizate în ecuațiile pentru măsurarea directă a argumentelor.
Eroare sistematică constantă Δc din rezultatul măsurării indirecte
Dacă semnele unor erori sistematice specifice ci sunt necunoscute, atunci eroarea sistematică a rezultatului măsurărilor indirecte se găsește ca
care se numește limita.
La calculul erorilor relative, sistemul de expresii pentru c și
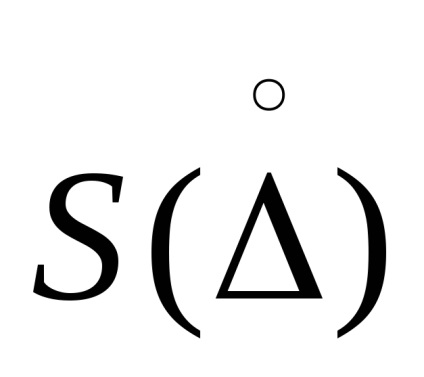
Trebuie remarcat faptul că eroarea relativă a măsurătorilor indirecte poate, în unele cazuri, să obțină valori foarte mari, de exemplu, pentru o funcție a formei Q = Q1-Q2 pentru valori mici ale diferenței
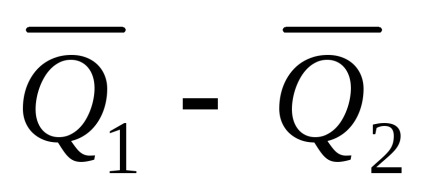
În cazul măsurărilor indirecte, este necesar să se dezvolte metode care să asigure păstrarea erorii măsurării indirecte în limitele admise. Acest lucru este realizat prin alegerea valorilor Ql și Qk. în care eroarea relativă nu depășește limitele admisibile; utilizarea metodelor de măsurare în care ecuația măsurării indirecte nu conține diferențe mici; dezvoltarea metodelor și a mijloacelor de măsurare, care oferă o măsurătoare directă în locul unei metode indirecte.
Să analizăm modul în care se estimează intervalul de încredere al erorii aleatorii și limita sau intervalul de încredere al erorilor sistematice care nu sunt excluse din rezultatul măsurătorilor indirecte.
O eroare aleatoare în rezultatul unei măsurări indirecte poate fi privită ca o variabilă aleatoare distribuită în mod normal, chiar dacă termenii au o distribuție diferită de cea normală, dar numărul de termeni este cel puțin 4-5 și nu există o eroare dominantă.
Limitele de încredere p ale erorii aleatorii sunt determinate de formula
factor
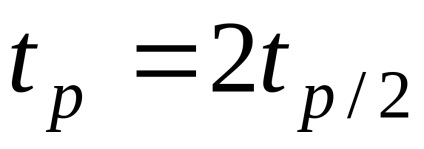
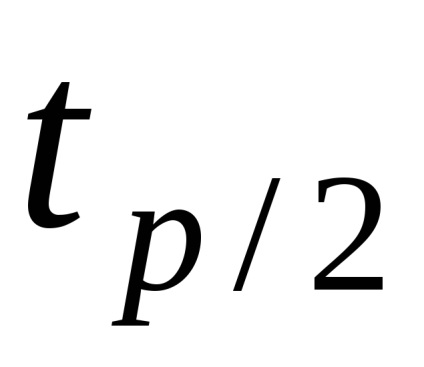
După cum sa menționat mai sus, erorile sistematice care nu sunt excluse pot fi considerate variabile aleatoare. Pentru fiecare dintre componente, se găsesc limitele lui i și, dacă este posibil să se justifice rezolvarea distribuției și estimarea
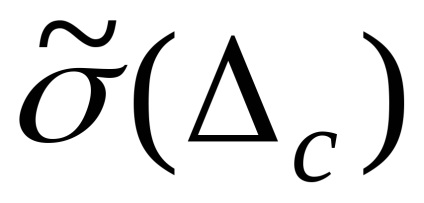
unde k este coeficientul determinat de probabilitatea de încredere presupusă, care pentru probabilitățile de încredere este de 0,9; 0,95; 0,99 sunt respectiv 0,95; 1.1; 1.4.
Limitele erorii totale de măsurare sunt estimate în conformitate cu GOST 8.207-76 [7].