Pentru a rezolva problemele de maximizare, pot fi utilizate două abordări.
Podhod1. Transformarea problemei de maximizare într-o problemă de minimizare echivalentă prin înmulțirea funcției obiective cu -1 și apoi aplicarea metodei simplex la problema minimizării.
Abordarea 2. După cum sa arătat mai sus, estimările relative din linia pj reprezintă schimbarea funcției obiective f ca variabila non-variabilă să scadă cu una. Coeficientul negativ din linia pj indică o descreștere în f pe măsură ce variabila non-azală corespunzătoare crește.
Prin urmare, pentru problemele de maximizare, variabilele non-aleatoare xj cu pj pozitiv trebuie să fie introduse în bază. deoarece ele îmbunătățesc funcția obiectivă. Dacă toți coeficienții din șirul pj sunt negativi sau egali cu zero, soluția curentă este optimă.
Exemplul 6.9. Rezolvați simplexul prin metoda problemei:
Soluția. Cu ajutorul unor variabile non-negative suplimentare, trecem la sistemul de ecuații. În acest caz, toate variabilele suplimentare sunt introduse cu semnul "+", deoarece toate inegalitățile au forma "".
Obținem un sistem de constrângeri în forma:
Activitatea 1.
Presupunând variabilele libere x1 în egalități (6.37). x2 egal cu zero, aflăm. . . . și anume soluția de bază x 0 = (0; 0; 18; 16; 5; 21). Deoarece toate variabilele de bază la x 0 sunt pozitive, această soluție de bază este admisibilă (punct de colț) și nondegenerat. Folosind abordarea 1, ne îndreptăm atenția asupra problemei de minimizare
Folosind egalitățile (6.35) și (6.36), compunem o tabelă simplex corespunzătoare punctului unghiular x 0:
În conformitate cu paragraful 4 al algoritmului, verificăm criteriul de optimitate. Ultimul rând conține coeficienți negativi. Alegem modulul cel mai mare (-3); a doua coloană de rezolvare, variabila x2 va merge la coloana principală (această coloană este marcată cu o săgeată). În conformitate cu alineatul (5), găsim rapoartele estimate și. A treia linie este rezolvată (marcată cu săgeată orizontală). La intersecția rândurilor și coloanelor de rezolvare, există un element de susținere (înconjurat de un cadru).
2. Construim masa conform regulilor din pasul 6 al algoritmului (Tabelul 6.10). În noua bază, variabilele principale sunt :.
Criteriul de optimitate nu a fost găsit din nou. Acum, prima coloană este rezolvată; x1 - trecerea la principalele ,; prima linie este rezolvarea, - elementul de susținere.
Tabel simplă pentru punctul de colț x 1
3. Noua tabelă simplex va lua forma (Tabelul 6.11).
Tabel simplă pentru punctul de colț x 2
Și de această dată criteriul de optimitate nu este îndeplinit; Cea de-a doua coloană și a doua linie sunt cele care rezolvă problema, elementul de susținere.
4. Mergeți la Tabelul 6.12.
Tabel simplă pentru punctul unghiular x 3
Criteriul de optimitate este îndeplinit, deci f * = f (x *) = 24, soluția de bază optimă x * = (6,4,0,0,1,1,3).
Soluția grafică a problemei este prezentată în Fig. 6.10, de unde este clar că x * = (6; 4) și f * = f (x *) = 24.
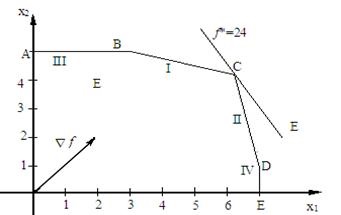
Fig. 6.10. Soluția grafică a problemei 6.19