Porniți conectorul "Cronometru" în priza de 220 V.
Activați tasta "Rețea" de pe spatele "Cronometru" (tasta este aprinsă).
Setați sarcina la înălțime. care corespunde gamei de rigle. Porniți electromagnetul (butonul din partea de sus a instalației)
Eliminați rularea încărcăturii.
Măsurați înălțimea încărcăturii pe riglă.
Apăsați butonul "start" de pe afișajul "Cronometru".
Înregistrați timpul deplasării încărcăturii în punctul cel mai de jos.
Notă: sarcina trebuie să cadă pe țintă situată pe suprafața bazei.
Lecția 3. Legea dinamicii mișcării rotative
OBIECTIV: studierea legii dinamicii mișcării de rotație, reprezentarea grafică și prelucrarea rezultatelor măsurătorilor.
Parametrii cinematici și dinamici de bază ai mișcării de rotație:
φ - calea unghiulară sau unghiul de rotație;
Pentru un punct arbitrar al unui corp rotativ localizat la o distanță r de axa de rotație, modulul de viteză liniară
și modulul de accelerație tangențială
Modulul de cuplu al tensiunii firului, înfășurat pe o roată de rază r,
Momentul momentului momentului unui punct material de masă m, care se deplasează cu viteza v, la o distanță r față de axa de rotație:
Pentru un corp cu un moment de inerție I. care se rotește cu viteza ω, modulul momentului momentului
Momentul de inerție al unui punct material de masă m, scos din axa de rotație cu o distanță r, I = mr2.
Momentul inerției corpului față de axa selectată este egal cu suma momentelor de inerție ale tuturor punctelor N ale corpului:
Legea dinamicii mișcării de rotație
Dacă momentul inerției corpului rotativ rămâne constant, atunci legea dinamicii ia forma
Dați definiția mărimii accelerației unghiulare.
Ce se numește momentul forței?
Care este ritmul unghiular al corpului?
Care este momentul inerției unui punct material?
Care este momentul inerției corpului?
În ce unități se măsoară accelerația unghiulară, momentul forței, momentul inerției, impulsul unghiular?
Formulează legea dinamicii mișcării de rotație.
Notați legea dinamicii mișcării de rotație a cazului atunci când momentul inerției unui corp rotativ nu se schimbă.
În ce scopuri sunt folosite graficele?
Din ce motive alegeți mărimea axelor pentru diagramă?
Ce indicați pe axele graficului?
Cum alegi limitele intervalului pe grafice?
Cum de a alege scala axei numerice a graficului? Cum este indicat?
Cum se trasează curba experimentală pe grafic?
Prin ce punct este necesar să se traseze o linie dreaptă pe grafic, dacă dependența este liniară?
Cum este panta determinată de conducătorul dependenței?
Cum se găsește eroarea aleatorie a coeficientului unghiular?
Care surse de eroare aleatorie duc la o "împrăștiere" a punctelor pe grafice atunci când studiază mișcarea?
Lucrarea nr. 3. Studiul legii dinamicii mișcării de rotație
cu ajutorul pendulului Oberbeck
OBIECTIV: obținerea dependenței experimentale a accelerației unghiulare la momentul forței și determinarea momentului de inerție a pendulului printr-o metodă dinamică.
ECHIPAMENTE: pendulul Oberbeck, cronometrul, caliperul, rigla, setul de sarcini.
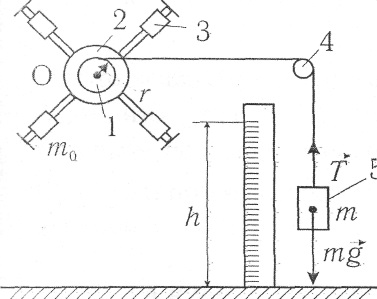
Partea principală a instalației este un pendul în formă de cruce, care se poate roti cu frecare mică în jurul axei O (a se vedea figura).
Cilindrii mobili 3 ai masei m0 se pot deplasa de-a lungul tijei păianjenului. Pe aceeași axă cu roțile trapezoidale 1 și 2 de rază diferită r sunt instalate. La capătul filetului, înfășurat pe una dintre scripeți și aruncat prin blocul fără greutate 4, este atașată o sarcină 5 de m masă, conducând pendulul în mișcare rotativă. Timpul de tranzit pentru distanța h este măsurat cu un cronometru. Pendulul în poziția inițială este ținut de electromagnet, când tasta "Start" este apăsată, electromagnetul este deconectat, sarcina începe să se miște și cronometrul începe simultan. Contorul de timp se termină când încărcătura ajunge în poziția de jos. Pentru ca cronometrul să funcționeze, este necesar să se stabilească cu ajutorul șuruburilor de la baza platformei o poziție în care sarcina ar cădea exact în cercul marcat. În acest cerc este montat un senzor care oprește cronometrul.
Distanța h este indicată de rigla instalată în partea superioară a instalației, ceea ce indică distanța încărcării în poziția inițială de la baza instalației.
DESCRIEREA METODEI DE MĂSURĂRI
Presupunând că firul este greu, inextensibil, considerăm că mișcarea bunurilor este la fel de accelerată. Accelerația încărcăturii a este determinată prin măsurarea timpului de deplasare și a traseului traversat h.
Accelerația unghiulară a pendulului α este exprimată în termeni de accelerație liniară și raza roții:
Tensiunea firului T poate fi determinată prin aplicarea legii lui Newton la mișcarea masei m (neglijând rezistența aerului):
Astfel, prin măsurarea pentru o încărcătură de masă m a timpului t de trecere a distanței h de ea. este posibil să se calculeze accelerația unghiulară α (formula 10) a pendulului și să se determine momentul forței care acționează asupra pendulului:
Când pendulul este rotit, cuplul de frânare al forțelor de frecare ale MTP acționează de asemenea asupra acestuia. și prin urmare legea dinamicii (2.8) ia forma
Această ecuație face posibilă găsirea momentului de inerție al blocului I prin metoda dinamică, măsurând un număr de valori ale lui α și M. Pentru o determinare mai precisă a valorii lui I, se obține dependența α = f (M) în experiment. a cărui caracter liniar (cu
MTP = const) face posibilă calcularea valorii medii a lui I din coeficientul unghiular al liniei experimentale.
Sarcina 1. Studiul legii de rotație a pendulului
1. Determinați masa mărfurilor t, stabiliți centrele cilindrilor mobili m0 la aceeași distanță l față de axa de rotație și măsurați razele rolelor r1 și r2. Rezultatele sunt scrise în tabel. 1.
3. Atașați una dintre sarcinile t la fir. Rotiți pendulul, înfășurați firul pe scripetele mici r1 într-un singur strat și porniți electromagnetul cu butonul roșu situat în partea superioară a unității. Înregistrați distanța h. traversat de încărcătură în toamnă. Asigurați-vă că firul și încărcătura nu ating piese staționare ale instalației sau alte obiecte în timpul conducerii. Eliminați rotirea încărcăturii și apăsați butonul "Start" al cronometrului. Înregistrați timpul t pentru deplasarea încărcăturii în punctul cel mai de jos.
Cu aceeași roată, crescând masa sarcinii t (de cel puțin 4 ori), înregistrați timpul t al mișcării încărcăturii pe calea h. Toate rezultatele obținute sunt înregistrate în tabelul. 1.
Măsurătorile similare sunt efectuate folosind o roată cu rază r.
Calculați valorile lui a și M în fiecare experiment folosind formulele (10, 11).
Utilizați recomandările din 3.1, prezentați grafic dependența accelerației unghiulare a la momentul forței M, reprezentând punctele pentru ambele scripeți pe un singur grafic.
Din grafic, determinați valoarea medie a momentului de inerție al pendulului I = ΔM / Δα, calculând panta liniei drepte.
Conform planului, determinați momentul forțelor de frecare, comparați-l cu momentele create de sarcini și trageți o concluzie.
10. Calculați coeficientul ΔI relativ și ΔΙ absolut al momentului erorii de inerție (a se vedea instrucțiunile din paragraful 3.3);
11. Înregistrați rezultatul sub forma unui interval de încredere
cu probabilitatea de încredere P. estimată prin formula (4).
Sarcini e 2. Măsurarea prin metoda dinamică a momentului de inerție a traversei pendulului
1. Asigurați cilindrii mobili la o distanță maximă și aceeași la l față de axa de rotație. Atașați o sarcină de masă m la fir. Selectați o rotiță pentru experiment, măsurați raza și scrieți-o în tabel. 2 valorile lui m, rih.
2. Rotiți pendulul, înfășurați firul pe scripete într-un singur strat și măsurați timpul t (vezi punctul 3 din sarcina 1).
5. Efectuați încă 6 experimente cu aceeași greutate, micșorând distanța cilindrilor l de la axa de rotație cu câte 1,5-2 cm de fiecare dată. Rezultatele măsurătorilor lui l și t sunt prezentate în tabelul. 2.
4. Se calculează pentru fiecare experiment cantitățile 12 și momentul inerției pendulului conform formulei obținute cu toleranța expresiilor (10), (11):
5. Construiește un grafic al dependenței momentului de inerție a pendulului I de 12 (vezi recomandările din 3.1). Se va deduce natura dependenței obținute I = f (12), ținând seama de faptul că momentul inerției pendulului, pentru care cilindrii sunt luați ca puncte materiale,
6. Determinați, utilizând graficul (metoda dinamică), momentul de inerție al crucii Icr. care în conformitate cu (14) este egal cu parametrul b al dependenței liniare I = f (12).
7. Calculați masa încărcăturii suspendate m0. 8. A trage concluzii.
1. Scrieți legea dinamicii mișcării de rotație.
2. Ce rotație a corpului se numește la fel de accelerată, care sunt condițiile sale? 3. Cum sunt direcționați vectorii, impulsul unghiular al corpului?
4. În ce constă (a) accelerația unghiulară a pendulului, (b) momentul inerției pendulului, (c) momentul forței care acționează asupra pendulului?
Care dependență stă la baza metodei dinamice de măsurare a momentului de inerție I?
Care sunt valorile pantei liniei din grafic α = f (M)?
Cum în lucrare se schimbă momentul forței?
Ce valori ale lucrării sunt măsurate pentru a determina valorile lui α și M?
Cum poți schimba momentul inerției unui pendul în această lucrare?