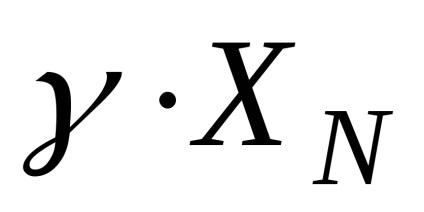3.5.1. O singură măsurătoare cu o estimare exactă a erorii
Majoritatea covârșitoare a măsurătorilor este una singură. Rezultatele măsurătorilor includ componente instrumentale, metodologice și personale, fiecare dintre acestea putând fi sistematic și aleator.
Erorile sistematice într-un fel sau altul încearcă să excludă, să rămână NSP și erorile aleatorii.
Limitele NSP se calculează de la formula dată anterior (3.8).
În cazul în care măsurătorile repetate ale limitelor anterioare de încredere cunoscute de eroare aleatoare e, apoi se adaugă la SNR, SNR este considerat ca fiind o eroare aleatoare. Eroarea totală limitată de eroare Δ este determinată de formula:
Dacă ε nu este cunoscută, atunci ε = 0 este presupusă.
Rezultatul unei singure măsurători a lui R, cu o valoare măsurată de X, este reprezentat ca:
3.5.2. Masurare unica cu estimarea aproximativa a erorii
Aproximativ eroarea de măsurare este evaluată "de sus", cunoscând limita erorii admise a instrumentului de măsurare Δpr din pașaport. De multe ori, ca urmare a valorii limită de eroare de măsurare ia Δpr = ± (jumătate din prețul diviziei de unități), și, uneori, Δpr = ± (împărțirea prețul unitar).
Eroare de măsurare a erorilor
Definiția măsurărilor indirecte este dată în subsecțiunea 2.1. Calcularea erorilor măsurărilor indirecte poate fi redusă la reguli simple [4], care indică: R este rezultatul măsurărilor indirecte; A, B, C este rezultatul măsurărilor directe ale parametrilor pe baza cărora se calculează R; Δ - eroare absolută de măsurare a oricărei valori, de exemplu ΔR, ΔA etc .; δ - eroare relativă a valorii, de exemplu: δR = ΔR / R; ΔA = ΔA / A și așa mai departe.
Dacă R = A + B sau R = A - B. atunci
adică eroarea absolută a rezultatului măsurării indirecte este egală cu suma erorilor absolute ale rezultatelor măsurătorilor directe.
Dacă R = A · B sau R = A / B, se adaugă erorile relative:
Dacă R = kA. unde k este un coeficient, atunci
unde | k | Este valoarea absolută a coeficientului.
Un exemplu. Puterea P. extrasă dintr-un rezistor cu rezistență R la un curent I este I2 · R. Apoi eroarea relativă δP = 2 · δI + δR. Eroarea absolută a rezultatului ΔР = δP / Р. Rezultatul va fi prezentat ca: P ± ΔP.
Eroare la instrumentul de eroare
Aparatele de scalare (analogice) sunt utilizate pe scară largă în măsurători [9]. Scala unuia dintre instrumente este prezentată în Fig. 3.4. În partea inferioară a scalei, numărul 2 înseamnă clasa dispozitivului, aici sunt plasate și alte simboluri speciale.
P
Eroarea absolută a mijloacelor de măsurare Δ se determină ca diferență în citirile măsurătorilor X și în citirile instrumentului de referință Het:
Fig. 3.4. Scala dispozitivului
Eroarea absolută este o valoare dimensională. Corecția la aceasta este egală cu eroarea absolută cu semnul opus.
Eroarea relativă este determinată de ecuațiile:
Eroarea relativă este o cantitate fără dimensiuni și poate fi exprimată ca o fracție zecimală sau ca procent.
Eroarea relativă redusă este definită ca raportul dintre eroarea absolută a instrumentului și valoarea normalizată a scalei (până la limita superioară a măsurătorii) XN:
Eroarea relativă relativă în procente determină clasa de precizie a dispozitivului.
Un exemplu. Pentru cel prezentat în Fig. 3.4 din clasa de exactitate 2, eroarea redusă γ a fost 2% = (0,02). Apoi, eroarea absolută a indicațiilor Δ =