Unda electromagnetică este un val generat de oscilația parametrului câmpului electromagnetic.
Mișcarea valurilor este însoțită de transferul energiei din sursa de oscilație spre diferite puncte ale mediului (figura 4.1). Această energie constă din
Transferul energiei printr-un val (Figura 4.1)
energia cinetică a particulelor oscilante și energia potențială a părților deformate ale mediului. Energia purtată de o undă printr-o anumită suprafață pe unitate de timp se numește fluxul de energie prin această suprafață.
Lăsați secțiunea valului S din față cu o zonă în timp să se deplaseze de la distanță. ca urmare a faptului că particulele mediului în volumul cilindrului sunt ridicate de înălțime și de baza S într-o mișcare oscilantă. Să denotăm prin energia medie a particulelor conținute într-un volum de unitate (densitatea de energie). Dacă presupunem că densitatea energetică este aceeași peste tot, atunci prin timp energia trece prin:
Apoi intensitatea valului este egală cu:
sau în forma vectorială:
Densitatea fluxului de energie sau intensitatea undei se spune cantitatea de energie transportată de către unda pe unitatea de timp prin unitatea de suprafață, perpendicular pe direcția de propagare a undei, măsurată în W / m 2. Densitatea fluxului de energie coincide cu direcția de propagare a energiei valurilor.
Densitatea în vrac a energiei câmpului electrostatic - e mărimea fizică este numeric egal cu raportul dintre energia câmpului potențial conținut în elementul de volum, la acest volum. Pentru câmp omogen densitatea de energie este volumul. Pentru un condensator plat al cărui volum Sd, unde S - suprafața plăcilor, d - distanța dintre plăci, avem:
5. Exemple de sarcini de testare pe tema "Oscilații și valuri mecanice și electromagnetice"
Mingea, atașată la arc și montată pe o șină orizontală, efectuează oscilații armonice.
Graficul arată dependența proiecției forței arcului de arc pe direcția pozitivă a axei X de coordonatele mingii.
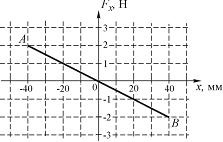
Lucrarea forței elastice atunci când mingea se deplasează de la poziția B la poziția A este egală cu ...
0 J 8 · 10 -2 J 4 · 10 -2 J -4 · 10 -2 J
Lucrarea forței elastice atunci când bila se deplasează de la poziția B la poziția A este egală cu:
Două oscilații armonice de aceeași direcție cu aceleași perioade și amplitudini egale sunt adăugate. Cu diferența de fază, amplitudinea oscilației rezultate este ...
Amplitudinea rezultată este
A = (4 * A0 * cos 2 (# 8710, # 966;)) 2 = 1/2 * A0 * (cos (3 * / 2)) 1/2 = 2 * A
Figura prezintă o imagine instantanee a componentei electrice a undei electromagnetice, care trece de la mediul 1 la mediul 2 perpendicular pe interfața AB.
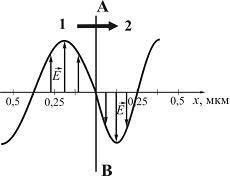
Raportul dintre viteza luminii în mediul 2 și viteza sa în mediul 1 este ...
Frecvența oscilației undelor luminoase în orice mediu este constantă. Aceasta înseamnă că raportul dintre viteza luminii în mediul 2 și viteza sa în mediul 1 este egal cu raportul dintre lungimea undei luminoase în mediul 2 și lungimea de undă în mediul 1.
Dacă densitatea volumului de energie este dublată și viteza de propagare a undelor elastice este redusă cu un factor de 2, atunci densitatea fluxului de energie este ...
Creșteți de 2 ori scăderea de 2 ori va rămâne neschimbată
j = w * v =. Prin înlocuirea datelor din problemă cu formula, obținem j = 2w * v / 2 = w * v
Punctul material efectuează oscilații armonice conform legii. Valoarea maximă a punctului de accelerare este ...
1) m / s 2 2) m / s 2
3) m / s 2 4) m / s 2
Răspuns: 2, al doilea derivat al coordonatei este accelerarea,
Se adaugă două oscilații armonice de aceeași direcție cu aceleași frecvențe și amplitudini egale. Cu diferența de fază, amplitudinea oscilației rezultate este ...
Răspuns: 1 ,. se aplică metoda diagramelor vectoriale. Unghiul dintre vectori este de 90 ° și adăugarea oscilațiilor este suma geometrică a acestor vectori.
Ecuația unei valuri sinusoidale plane propagând de-a lungul axei OX are forma. Lungimea de undă este ...
1) 2 m 2) 3,14 m 3) 1000 m
Răspuns: 2 ,. Se poate observa din formula că viteza v = 500 m / s, frecvența ciclică # 969; = 10 3 rad / s. # 955; = 2 · 3,14 · 500/10 3 = 3,14 m.
Dacă reducem densitatea în vrac a energiei cu un factor de 2 cu viteza de propagare a undelor elastice neschimbate, atunci densitatea fluxului energetic ...
1) rămâne neschimbată 2) scade cu un factor de 2
3) va scădea de 4 ori
Răspuns: 2, # 969; = W / V, W = # 969; V. Cu densitate în vrac crescândă # 969; De 2 ori, W crește de asemenea de 2 ori.
Literatură recomandată pentru pregătirea pentru examenul online