Efectul de diminuare a fost detectat de către Joel și Thomson într-un mod experimental în 1852. [Experimentele au stabilit că temperatura lichidului de lucru se modifică ca urmare a reducerii. Acest fenomen a fost numit efectul Joule-Thomson. Schimbarea temperaturii în timpul reglării se datorează faptului că în fiecare gaz real se manifestă forțele de atracție și repulsie între molecule. Când presiunea de gazare se extinde, însoțită de o creștere a distanței dintre ele. Toate acestea conduc la o scădere a energiei interne a fluidului de lucru, asociată cu costul muncii, care, la rândul său, conduce la o schimbare a temperaturii.
Temperatura ideală a gazului nu se modifică ca rezultat al reglării, iar efectul Joule-Thomson în acest caz este zero. Astfel, schimbarea temperaturii unui gaz real în timpul diminuării este determinată de devierea proprietăților gazului real de la gazul ideal, care se datorează acțiunii forțelor intermoleculare.
Sunt distincționate ambreiajele de temperatură și de temperatură integrale. Cu efectul diferențial Joule-Thomson, temperatura se modifică cu o valoare infinitezimală, iar pentru un efect integral, temperatura se modifică cu o valoare finită. Dacă presiunea gazului scade cu o cantitate infinitezimală dp, atunci apare o schimbare de temperatură infinitezimală, adică dTi = ai dpi sau
Cantitatea ai este numită efectul de temperatură Joule-Thomson diferențial. Valoarea lui a, poate fi determinată din ecuație (vezi § 5.48)
Ținând cont de faptul că atunci când nu există schimbări în entalpia (di = 0), semi-chim
Efectul clapetei poate fi pozitiv, negativ și egal cu zero. Un efect pozitiv al șocului apare atunci când temperatura gazului scade cu picăturile. Negativ - cand iesi afara. În cazul temperaturii neschimbate în timpul reglării, se observă efectul zero Joule-Thomson. Starea gazului real în reglaj, atunci când efectul de reglaj este zero, se numește punctul de inversiune. În acest moment, semnul efectului de temperatură se modifică. Dacă temperatura gazului de gaz este presată sub temperatura de inversiune, gazul se răcește atunci când este presurizat, dacă crește mai mult, se încălzește.
Pentru a găsi condițiile în care temperatura gazului se schimbă sau rămâne neschimbată, este necesar să se analizeze ecuația (7.19) scrisă în formular
Atunci când dp <0, так как давление газа всегда уменьшается. Теплоемкость ср - величина положительная. Отсюда следует, что знак dT
depinde de semnul expresiei și este întotdeauna opusul acesteia.
pentru T (dv / dT) p - v = 0 dT = 0. Cazul în care dT = 0 poate fi folosit pentru
obținerea temperaturii de inversiune.
Ultima expresie se numește ecuația curbei de inversiune (o curbă pe care efectul de reglaj este zero).
Efectul integral Joule-Thomson este determinat prin integrarea ecuației (7.20)
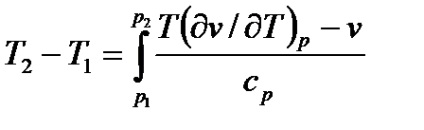
În inginerie, este adesea necesar să se trateze substanțe gazoase, care reprezintă un amestec mecanic de gaze individuale, care în proprietățile sale aproximează gazele ideale.
De exemplu, aerul atmosferic este un amestec de gaze care include azot, oxigen, dioxid de carbon, vapori de apă și o serie de alte gaze. Determinarea parametrilor este necesară pentru rezolvarea multor probleme practice.
Un amestec de gaze este un amestec de gaze individuale care nu reacționează chimic unul cu celălalt, adică fiecare gaz în amestec se păstrează pe deplin toate proprietățile sale și ocupă întregul volum al amestecului. Presiunea creată de fiecare moleculă individuală a amestecurilor de gaze, cu condiția ca gazul este una în aceeași sumă, în aceeași cantitate și la aceeași temperatură ca și amestecul numit presiune parțială (parțială).
Presupunem că fiecare gaz individual al amestecului respectă ecuația (2.7), adică este un gaz ideal. Prin urmare, parametrii amestecului de gaz pot fi de asemenea calculați din ecuația Clapeyron
unde toate cantitățile din această ecuație se referă la un amestec de gaze.
Conform legii lui Dalton, presiunea totală a unui amestec de gaze ideale este egală cu suma presiunilor parțiale ale gazelor care intră în amestec
unde p este presiunea amestecului; presiuni parțiale ale gazelor de amestec individuale.
Amestecul gazos poate fi specificat prin fracții de masă, volum și molar.
Fracția de masă - raportul dintre masa fiecărui gaz individual și masa totală a amestecului
Suma fracțiunilor de masă este una
Fracțiunea de volum este raportul dintre volumul parțial (redus) al fiecărui gaz și volumul total al amestecului
gaze; V este volumul amestecului de gaze.
Volumul parțial este volumul care ar ocupa gazul dacă presiunea și temperatura acestuia ar fi egale cu parametrii amestecului de gaze.
Volumul parțial al fiecărui gaz la o temperatură constantă se regăsește în legea Boyle-Mariotte
Adăugând aceste ecuații termen pe termen, constatăm că suma volumelor parțiale este egală cu volumul amestecului (Legea Amaga)
Dacă adăugăm fracțiile de volum, obținem
Din legea lui Boyle-Mariotte (la o temperatură constantă) urmează pi / p-Vi / V. De aici
Ultima formulă permite determinarea presiunilor parțiale ale componentelor unui amestec dacă este cunoscută compoziția volumului acestuia.
Specificarea amestecului cu fracții molare este după cum urmează. Mai întâi găsim numărul de moli ai fiecărei componente a amestecului în funcție de relații
unde M1. M2. .... Mn este numărul de moli ai fiecărei componente; μ1. μ2, ..., μn sunt greutățile moleculare ale componentelor corespunzătoare ale amestecului.
Prin urmare, întregul amestec de gaze va conține moli M
Fracțiile molare yi (i = 1,2,3, ..., n) sunt sub formă de relații
Deoarece M = m / μ, greutatea moleculară a amestecului μ va fi determinată prin formula
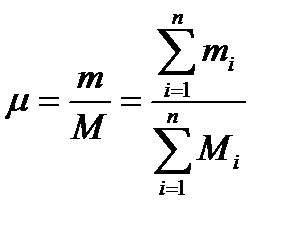
Valoarea obținută se numește valoarea medie aparentă a greutății moleculare a amestecului. Cunoașterea greutății moleculare face posibilă găsirea constantei de gaz a amestecului R prin formula (2.9a) R = 8.3143 / μ (formula pentru determinarea lui μ prin R cunoscută va fi dată mai jos).
Conform legii lui Avogadro, volumul molar al diferitelor gaze la presiuni și temperaturi egale este egal (cantități egale de gaze diferite conțin același număr de molecule). Prin urmare, pentru gazul i al amestecului, relația
unde Vμ este volumul ocupat de un mol de gaz.
Pentru întregul amestec, ajungem
În consecință, fracțiile mol și volum sunt numeric egale.
Rezultă o formulă pentru determinarea greutății moleculare a unui amestec prin compoziția sa de volum. Din cea precedentă pentru componenta i, putem scrie
sau pentru întregul amestec
Înlocuind în ultima ecuație greutățile moleculare prin densitatea lor (pe baza legii lui Avogadro), obținem
În cazul în care amestecul de gaze este dat de compoziția de masă, atunci din ecuația de stare
Pentru presiunea întregului amestec, obținem formula
Având în vedere că pV = mRT, obținem
Utilizând amestecul cunoscut gaz constant, folosind formula (2.9a), se poate găsi masa moleculară a amestecului.