Orice noduri copac frate arbitrare sunt distanțate prin valoare setarea dinamică (în acest caz 20), precum și nodurile învecinate (în acest caz 40). În momentul în care se formează ramura din stânga, se face apel la metoda nodul-nod în care sunt transmise partea superioară stângă și cea superioară dreaptă, iar diferența dintre ele este mărită (în acest caz, 20).
Iată ce se întâmplă în metoda de descărcare a nodurilor -
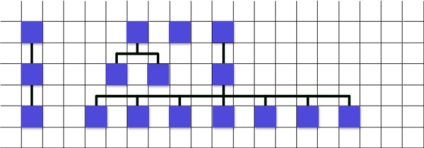
- în ciclul pe care îl trecem de la stânga sus la dreapta sus și luăm în considerare golurile (în acest caz, sunt șase celule goale, care, după cum sa spus anterior, au fost 20, adică suma de 120);
- Împărțim suma primită în etapa anterioară cu numărul de noduri plus un (120/3 = 40);
- Am verificat cât de mult este nodul curent (pornesc de la stânga la dreapta și deci nodul curent este cel cu doi copii) este eliminat din fratele nodului stâng (în acest caz este de 80).
- acum scad din 80 - 40 = 40, această valoare este distanța până la care voi mișca nodul curent să fie în locul potrivit.
- dacă această valoare (40) este mai mare decât cea pentru care distanța dintre cele două noduri extreme a crescut, această valoare devine mai mică. Asta este, calculat ca 40, dar este mai mult decât este permis și, prin urmare, valoarea se modifică cu 20.
- Mișc nodul.
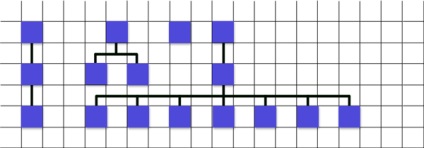
Repet sasele etape anterioare pentru urmatorul nod -
1. Am 60 de ani
2. 60/2 = 30
3. 40
4. 30
5. 10
6.
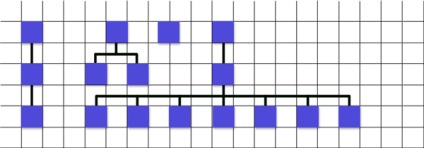
Vedeți modul în care am obținut media? În primul rând, dau seama de ce ai nevoie pentru a trece la patruzeci de ani, dar din moment ce patruzeci și mișcare, eu nu pot (încalcă drepturile copiilor la partea de jos, ei vor fi mai aproape de patruzeci), m-am mutat la maxima posibila este de douăzeci de ani. Și apoi mă schimb cu zece.
De exemplu, dacă primul nod procesat nu avea copii, atunci imaginea ar fi următoarea -
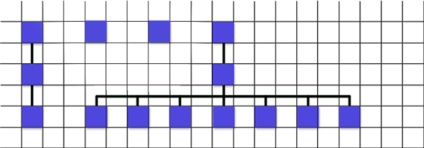
În cazul în care pentru prima oară am un nod care poate fi mutat "cumva" (fără copii) și după aceea care nu poate fi mutat "cumva", atunci mișc din nou cel de-al doilea la maximum, dar în același timp execut algoritmul de la început (mai exact, din ultimul punct de succes), dar pentru o vreme am înlocuit partea de sus-dreapta cu cea actuală.
Aș arăta codul, dar nu vreau să te uiți la neajunsurile lui, dar doar vrei să înțelegi semnificația.
Aici. " Dar apoi am intrat în următoarea problemă și poate e doar unul dintre ei.
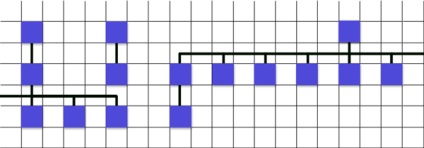
Intrarea este aceeași, dar totul se rupe. Algoritmul, așa cum am vrut, nu a funcționat și nu mă pot gândi la nimic.
Mai jos este rezultatul final -
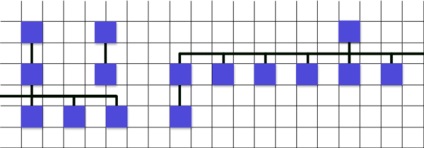
Care este nodul
indent - valoarea prin care nodul curent este eliminat din precedentul || -> | | |
leftOffset este valoarea la care mă deplasez spre stânga. Încă de la început este zero rightOffset = aceasta este valoarea prin care mă deplasez spre dreapta. Și, de asemenea, implicit la zero.
Aici. " Nodurile înseși, ca nodurile obișnuite, se referă la părinte, în care sunt stocate într-o matrice indexată. Există metode pentru obținerea nodului prin index și obținerea indexului în sine.
În general, este necesar să se organizeze nodurile deja de fapt, și să nu fie distorsionate de mișcarea într-un anumit cadru. Există două constante „frați“ și „vecini“, și „vecinii“ determină cât de mult ar trebui să fie distanțate subarbori adiacente pe niveluri mai mici decât prima, și „frații“ - prima. Apoi, problema trebuie rezolvată de jos în sus pentru fiecare subramificație mai întâi construiesc fiecare propriile lor subarbori, atunci noi construim curente poderevo calculate pentru fiecare din următoarele subramificație deplasare minimă în raport cu solul, în care, la fiecare nivel este subarbore nu va interfera cu subarbori deja stabilite. Ca urmare, fiecare poderevo va avea „intervalul ocupat“ la fiecare nivel, în cazul în care acesta are cel puțin o foaie și se va merge o comparație cu plasarea curentă a subarborelui la nivelul superior.
Ie algoritmul arată astfel:
dreapta este completat în felul următor: Dacă subdriga adăugată la nivelul i-m nu are un drept umplut, atunci la nivelul i + 1-m, dreapta nu se schimbă, dacă are, atunci dreapta devine egală cu decalajul expediat plus dreptul disponibil. stânga este umplută într-un mod similar, dar este umplută numai dacă nu este deja plină la acest nivel - de vreme ce noile subrețe sunt adăugate la dreapta, primul subtree cu adâncimea specificată va seta acest substrat la stânga. Atunci când pozițiaRoot () este executată, întreaga matrice dreapta și stânga este decrementată în funcție de poziție, după care se adaugă 0 la începutul matricelor.
Voi încerca să descriu desfășurarea algoritmului. Pentru a descrie arborele, voi folosi listele Lisp, numerele - foi, listele - subtreile. Exemplu: ((1) (2 3 4 5)) corespunde unui astfel de arbore:
Arborele original: (((1) 2) (((3))) ((4 5 6) ((7 8 9) (10)))). Eu nu consider subtreile dintr-o foaie, pentru că nu este nevoie. Subtreea ((1) 2) are valoarea: left = [0, -10, -10]; dreapta = [0,10, -10] și următoarea formă:
Asteriscurile denotă nodurile substraturilor, deoarece nu există elemente "rădăcină" în liste. Subfaza ((())) are o formă trivială, iar valoarea matricei rămase = [0,0,0,0]; dreapta = [0,0,0,0]. Substratul ((7 8 9) (10)) are valoarea matricelor left = [0, -30, -50]; dreapta = [0,30,30] și arată astfel:
Datorită faptului că subramificație (7 8 9) a obținut dreptul [1] ca 20 și compensate "vecini" 40, a doua subarborele a fost plasat la offset 60 (0 + 40 + 20), iar positionRoot a fost cauzată de un offset de 30 ( = 60/2), ca rezultat substratul stâng a eșuat în minus față de rădăcina comună cu -50. Construirea unui subtree 4-10 va arata astfel:
Limitatorul de poziție subarbore aici este al doilea strat, unde y (4 5 6) dreapta [1] = 20, și stânga [1] la -30 ° C subramificații, deplasarea totală totală este 90. La cel mai scăzut nivel al subarborelui stâng nici un element, deci noi trecem. Ca rezultat, positionRoot va fi apelat cu poziția 55, iar matricea generală arată ca left = [0, -55, -75.5]; dreapta = [0,55,85,85]. Apoi, asamblarea celor trei subramificații va fi construit după cum urmează: prima este plasat la offset 0, al doilea (((3))) la offset 50 și o mare a treia deplasare a 50 + 40 + (- 75) = 165, iar capul este deplasat de 87.5 . Total această imagine va fi:
Din cauza rotunjirilor al treilea rând între pinionul 4 și patru spații în loc de trei (am considerat un simbol = 10 puncte, dar am considerat că elementele care nu au lățime, astfel încât în loc de 20 și 40 în cauză trebuie să fie puse constantele 40 și 60).
Sper, explicat clar.
Actualizare: punct de vedere tehnic, puteți după subramificații de distribuție, astfel caută acele subarbori care pot fi deplasate în interiorul ecranului, fără a interfera cu restul, iar dacă problema este aici, atunci într-adevăr nu este, pentru că după plasarea subramificații obținut versiunea cea mai compactă a plasarea întregului copac lățime, și dacă unele subtrees pot fi mutate, adică. au o serie de poziții permise, puteți utiliza algoritmul pe care îl aveți. Și faptul că arborele ca rezultat este foarte greoi în lățime, aceasta nu este o problemă per se.