O funcție este numită funcție periodică. dacă există un număr. astfel încât egalitatea
Graficul grafic al unei funcții periodice are secțiuni repetate pe fiecare interval de lungime T. Cel mai mic dintre numerele T este numit cea mai mică perioadă a funcției. Implicit, litera T desemnează cu precizie cea mai mică perioadă, (figura 47).
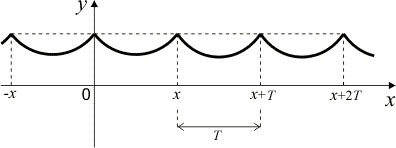
O investigație a funcției periodice și a construcției graficului acesteia trebuie efectuată pe un interval a cărui lungime este egală cu cea mai mică perioadă a funcției; Acest interval este denumit adesea intervalul de bază pentru o funcție periodică.
Mai jos sunt enumerate câteva proprietăți ale funcțiilor periodice.
O funcție periodică nu poate fi definită pe un set delimitat mai sus sau delimitat de mai jos.
De exemplu, funcția. nu este periodic.
Dacă numărul este o perioadă a unei funcții. apoi numărul. în cazul în care. este, de asemenea, perioada sa.
De exemplu, funcția. este periodic, cu cea mai mică perioadă și număr. sunt, de asemenea, perioadele sale.
Dacă numărul este cea mai mică perioadă a unei funcții. atunci funcția este de asemenea periodică, iar cea mai mică perioadă este egală cu un număr.
De exemplu, funcția. este periodic și perioada cea mai mică este egală cu.
Când se adaugă două funcții periodice împreună cu același OOF, se obține o funcție periodică, iar perioada cea mai scurtă este împărțită de și pe. în cazul în care. Sunt cele mai mici perioade ale summandelor.
De exemplu, - periodic cu. Periodic periodic c. deoarece și.
Exemple (studiul periodicității funcțiilor)
1. Este funcția periodică? Care este perioada cea mai mica?
Se știe că funcția elementară de bază este periodică cu cea mai mică perioadă.
Să verificăm egalitatea pentru o funcție dată:
Prin egalitate, concluzionăm că această funcție este periodică cu perioada. Pentru a găsi cea mai mică perioadă, scădem gradul de expresie prin formula trigonometrică cunoscută :.
Acum avem suma a două funcții periodice:
în consecință, această funcție are cea mai scurtă perioadă; prin urmare, să investigheze proprietățile sale și să trateze graficul în mod suficient pe diferența principală, de exemplu, la. și apoi continuați periodic întregului OOF.
Răspuns: funcția este periodică cu cea mai mică perioadă.
2. Este funcția periodică?
Această funcție complexă nu este periodică, deoarece funcția sa intermediară nu este periodică. "distorsionează" acele valori ale argumentului x. pentru care aceleași valori ar avea o funcție.
Pentru a ilustra acest lucru, să verificăm localizarea zerourilor acestei funcții:
Avem setul de toate zerourile funcției:
Vedem că zerourile funcției sunt localizate periodic pe axa OX. Prin urmare, această funcție nu este periodică (deoarece altfel toate proprietățile sale, inclusiv zerouri, s-ar repeta periodic).
Răspuns: funcția nu este periodică.
3. Care dintre următoarele funcții este periodică?
1) funcția nu este periodică, deoarece egalitatea nu are, de exemplu, un punct. deoarece acest punct se datorează faptului că limita inferioară a OOF. (Fig.48);
2) funcția nu este periodică, deoarece egalitatea nu este valabilă, de exemplu, pentru un punct. (Fig.49);
3) funcția este periodică cu cea mai mică perioadă. care se vede clar din graficul din fig. 50;
4) funcția este periodică cu cea mai mică perioadă. care se vede clar din graficul din fig. 51;
Răspuns: numai funcțiile 3) și 4) sunt periodice.