FACIAL STEPS METHOD
- metoda de construire a schemei diferențiale stabile pentru rezolvarea ecuațiilor diferențiale matematice (în sensul numărului de operațiuni). Fizică.
Cu o creștere a dimensiunii problemei, numărul de operațiuni pentru obținerea unei soluții numerice crește atât ca urmare a creșterii numărului de puncte, cât și datorită logicii. dificultăți în elaborarea unui program de calcul. Pentru un sistem de ecuații diferențiale
unde este operatorul diferențial, u = u (x, t), x = (xt, .xn), scheme implicite absolut stabile de aproximare simplă
devin ineficiente în cazul problemelor multidimensionale. În unele cazuri, este necesar să se utilizeze pas de timp foarte mici, în prezența celuilalt onu +1 necesită constHN a (m) operațiuni în care N- puncte pe o singură măsurătoare, iar m este numărul de dimensiuni spațiale, și (t) crește puternic odată cu creșterea T.
Pentru a obține scheme de diferențiere economice stabile, se propun metode bazate pe următoarele idei:
1) divizarea schemelor de diferențe;
2) aproximarea factorizării;
3) divizarea (aproximarea slabă) a ecuațiilor diferențiale.
În cazul (1), circuitul respectiv diferența sunt (pentru simplitate doi pași fracționate luate și privit problema periodică Cauchy.): Schema de spargere:
schema aproximativă de factorizare:
scheme de aproximare slabă:
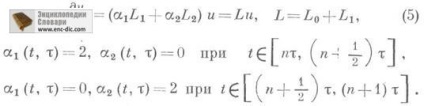
În cazul schemelor (3) și (4), inversarea operatorului se înlocuiește cu inversarea operatorului, adică printr-o inversare succesivă a operatorilor E, în general, a unei structuri mai simple.
Interpretarea (5) ne permite să luăm în considerare schema de divizare
ca o aproximare simplă a ecuației (5), care aproximează slab ecuația (1).
Astfel, în baza acestor metode este reprezentarea operatorilor complecși prin protozoare, în care integrarea ecuației inițiale reduce la integrarea ecuațiilor unei structuri mai simple și metode de pași fracționate sunt necesare pentru a îndeplini condițiile impuse de aproximare și stabilitate numai în final final (când le scrie într-un pași „întreg“ ). Metoda de divizare rezolvă multe probleme matematice complexe. Fizică.
O mare parte a dezvoltării a fost dată schemelor de divizare a unei ordini crescute de precizie. Pentru una dintre modificările metoda de divizare aparține metoda „particulelor în celule“: aici divizarea se face prin procedee fizice și nu este asociată cu o scădere a dimensiunii operatorilor.
Lit. : [1] Yanenko NN Metoda de pași fracționari pentru rezolvarea problemelor multidimensionale ale fizicii matematice, Novosib. 1967 [2] AA Samarskii, Introducere în teoria schemelor de diferențe, M. 1971.
Enciclopedia matematică. - M. Enciclopedia sovietică IM Vinogradov 1977-1985