Aveți grijă de articole noi din această serie.
Acest conținut face parte din seria: Lucrul cu structurile de date în limbile C și Python
Aveți grijă de articole noi din această serie.
Binarele binare (binare) reprezintă una dintre cele mai populare variante ale acestei structuri de date, deoarece sunt utilizate pe scară largă în algoritmii de căutare și pentru rezolvarea altor probleme de calcul. În acest articol, vom lua în considerare principalele caracteristici ale arborilor binari și diferitele operațiuni care sunt efectuate asupra lor.
Ca de obicei, în plus față de aspectele teoretice: clasificarea arborilor binari și tehnici standard pentru manipularea în articol sunt exemple de implementarea practică a algoritmilor pentru manipularea arbore binar în C și Python limbi.
Clasificarea copacilor binari
Înainte de a începe discuția despre diferite tipuri de arbori binari, merită să ne ocupăm de clasificarea generală a algoritmilor de căutare.
În cazul căutării liniare, elementul care trebuie căutat este comparat cu fiecare element al listei într-o iterație secvențială. Viteza unei astfel de căutări depinde de dimensiunea listei: cu cât este mai mare lista, cu atât viteza este mai mică, adică Viteza este invers proporțională cu dimensiunea listei. Puteți mări viteza unei astfel de căutări dacă sortați prima dată lista. În acest caz, nu mai trebuie să continue căutarea, atunci când elementul dorit nu a fost încă găsit, iar elementele din lista a devenit mai dorit.
Pentru o listă sortată există și un algoritm mai eficient. La începutul căutării, este necesar să se compare numărul cu elementul care este localizat ALTERNAT al listei deja sortate. Dacă elementul intermediar este mai mare decât numărul necesar, atunci elementul dorit este în jumătatea stângă. În caz contrar - în dreapta. Apoi, se face o comparație cu un număr care se află în mijlocul jumătății dorite. Și așa mai departe, până când se găsește numărul necesar. Acest tip de căutare se numește binar. și este evident mai rapid decât liniar. Numărul necesar de diviziuni dintr-o listă formată din n elemente în jumătate se numește logaritmul de la n la baza 2. Căutarea binară este un algoritm de ordin O (log) pentru baza 2.
Cu toate acestea, listele tradiționale legate nu sunt foarte potrivite pentru căutarea binară, iar un arbore binar vine la salvare, un exemplu al cărui exemplu este prezentat în Figura 1.
Figura 1. Exemplu de copac binar
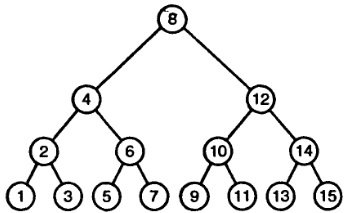

În general, fiecare nod dintr-un copac poate avea un număr nelimitat de noduri copil. Diferența dintre un arbore binar și alte tipuri de arbori este că fiecare nod din el nu poate avea mai mult de două noduri copil. Un arbore binar tipic este o structură constând din noduri, fiecare conținând o anumită valoare, precum și indicatori către substraturile din stânga și din dreapta. Unul sau ambii pointeri la aceste substraturi pot fi NULL. Copacii binari, ca listele legate, sunt structuri recursive.
Figura 2 prezintă copaci binari care au același set de noduri, dar o ordine diferită a secvenței lor. În ultimul caz, arborele se degenerează într-o listă conectată.
Figura 2. Diferite implementări ale aceluiași arbore binar
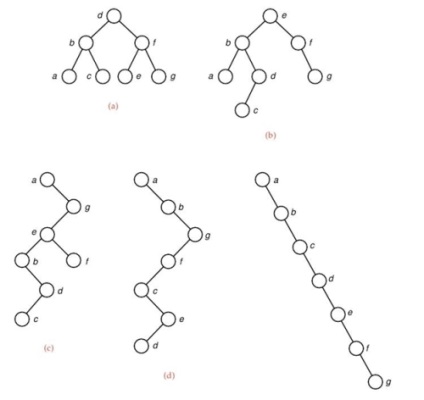

Există următoarele soiuri de copaci binari:
- arbore binar complet - fiecare nod, cu excepția frunzelor, are 2 noduri copil;
- un arbore binar ideal este un arbore binar complet în care toate frunzele sunt la aceeași înălțime;
- arbore echilibrat binar - acest arbore binar, în care o înălțime de 2 subarbori pentru fiecare nod nu diferă cu mai mult de 1. Adâncimea arborelui este calculat ca log logaritmului (n), unde n - numărul total de noduri;
- Un arbore degenerat este un arbore în care fiecare nod are un singur nod copil, de fapt, aceasta este o listă conectată;
- arbore binar de căutare (BST) - arbore binar în care fiecare nod condiție: toate nodurile din subarborele din stânga este mai mică, și toate nodurile din subarborele drept al nodului mai lung.
Calculul căilor
Calea (calea engleză) este distanța de la rădăcina arborelui la un nod. În arborele binar extins, fiecare cale se termină într-o foaie. Dacă numărul de frunze este notat cu S. și numărul de noduri rămase este notat cu N. atunci se aplică următoarea formulă:
și anume Pentru un copac extins, numărul de frunze pe unitate este mai mare decât numărul de NONLIVES (noduri care au noduri copil).
Dacă calea de la nodul rădăcină la frunza desemnată ca calea exterioară și calea de la nodul rădăcină să fie desemnat ca cale interioară NElista, atunci suma tuturor căilor externe pentru arborele prezentat în figura 3 este:
iar suma căilor interne va fi:
și apoi formula va conține:
unde n este numărul de noduri interne (NEListyev).
Figura 3. Exemplu de copac extins
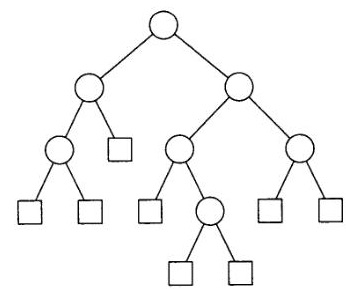

Să presupunem că există un set de frunze următoare:
Apoi putem formula următoarele sarcini:
- construi un arbore binar în așa fel încât suma căilor să fie minimă, deoarece aceasta reduce timpul de calcul pentru diferiți algoritmi.
- să construiască un copac binar extins complet astfel încât suma produselor din căile de la nodul rădăcină până la frunze să atingă valoarea nodului frunzelor este minimă.
David Huffman (David Huffman) a propus un algoritm pentru rezolvarea acestei probleme, în care cea mai mică de două prelatei sunt selectate și sunt adăugate în fiecare etapă, așa cum se arată în Listarea 1, ceea ce duce la arborele prezentat în figura 4.
Listarea 1. Un exemplu al algoritmului Huffman
Figura 4. Un arbore binar construit folosind algoritmul Huffman
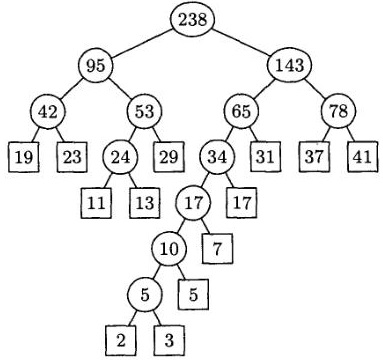

Codurile Huffman
Codurile Huffman sunt un algoritm folosit pentru a comprima date. Să fie un mesaj text original format din 5 simboluri: a, b, c, d, e. și fiecare simbol are propria frecvență:
Este necesar să codificați acest mesaj cu 0 și 1 astfel încât dimensiunea șirului rezultat să fie minimă. Tabelul prezintă un exemplu de codificare a caracterelor pentru acest mesaj:
Dacă criptați un mesaj folosind codul BCD №1, veți obține - 001010011. cu codul №2 poate face același lucru, dar șirul rezultat este mai scurt - 1101001.
Acum puteți formula însăși problema: trebuie să alegeți un algoritm de criptare, în care lungimea șirului criptat va fi minimă.
Într-un prim exemplu de realizare, fiecare caracter a fost dat de 3 caractere, iar în cea de a doua varianta - este 2.2, dar încă mai scurtă decât se poate face pentru a obține un factor de 2,15. Acest lucru se face folosind algoritmul Huffman, care are 2 simboluri cu cea mai mică frecvență și sunt combinate ca două noduri copil.
Algoritmul pentru un șir format din 5 simboluri este implementat după cum urmează. Primul pas combină două simboluri - a și d. ca având cea mai mică frecvență. Pe al doilea, simbolul c este adăugat ca părinte. În a treia etapă, se adaugă simbolul e. iar la sfârșit - simbolul b. Rezultatul este următorul cod:
Înălțimea copacului binar
Pentru a determina înălțimea copacului, trebuie să mergeți mai întâi de la rădăcină în subordonatul din stânga, apoi din dreapta, să comparați aceste două înălțimi și să selectați valoarea maximă. Și nu uitați să adăugați unitatea (elementul rădăcină) la valoarea rezultată. Lista 2 prezintă o funcție recursivă pentru această sarcină.
Listing 2. Determinarea înălțimii unui arbore este o implementare recursivă în C
Reflecția "oglindă" a unui copac binar
Atunci când doi arbori sunt o imagine oglindă unul de celălalt, se spune că ele sunt simetrice. Pentru a obține o copie "oglindă" a copacului, se folosește algoritmul din lista 3. În primul rând, se face o verificare a prezenței nodurilor copil în rădăcina copacilor și dacă aceste noduri există, schimbă locurile. Apoi, aceleași acțiuni sunt repetate repetat pentru nodurile copilului stâng și drept. Dacă există un singur nod copil, atunci puteți merge un nivel în jos pe copac și continuați.
Listing 3. Inversul unui arbore este o implementare recursivă în C
Căutați un nod într-un arbore binar
Pentru a căuta un nod dintr-un arbore binar pe baza valorilor conținute în el, puteți utiliza funcția de căutare. afișate în listare 4:
Listing 4. Găsirea unui nod într-un arbore este o implementare recursivă în C
Lățimea arborelui binar
Lățimea unui arbore este numărul maxim de noduri care se află la aceeași înălțime. Pentru a determina lățimea arborelui, pur și simplu adăugați contorul la algoritmul deja considerat a determina înălțimea arborelui.
Lista 5. Definirea lățimii unui arbore - o implementare recursivă în C
Numărul de noduri dintr-un arbore binar
De asemenea, puteți calcula numărul de noduri dintr-un arbore binar utilizând recursul.
Listing 6. Calculul numărului de noduri dintr-un arbore este o implementare recursivă în C
Comparația arborilor binari
Pentru a determina dacă doi copaci diferiți sunt aceiași, puteți folosi algoritmul în Lista 7.
Listing 7. Compararea arborilor binari - implementarea recursivă în C
concluzie
În acest articol a fost efectuată o clasificare a copacilor binari și s-au efectuat algoritmi pentru efectuarea celor mai importante operații: determinarea înălțimii și lățimii arborelui, reflectarea arborelui și căutarea unui anumit element în el. De asemenea, a fost considerat algoritmul Huffman, care poate fi utilizat pentru a construi copaci extinși și, ca o consecință, pentru a codifica informații.
Descărcați resurse
Subiecte conexe
- Lucrul cu structurile de date din C și Python. Partea 1.
- Lucrul cu structurile de date din C și Python. Partea 2.
- Lucrul cu structurile de date din C și Python. Partea 3.
- Lucrul cu structurile de date din C și Python. Partea 4.
- Lucrul cu structurile de date din C și Python. Partea 5.
- Lucrul cu structurile de date din C și Python. Partea 6.