Suprafața din poziția modului cinematic al formării sale este considerată ca fiind setul tuturor pozițiilor liniei (sau suprafeței) în mișcare. Cu această abordare la formarea suprafeței se poate argumenta că suprafața va fi definită (determinată), în cazul în care în orice moment, mișcarea va fi cunoscută în poziția sa de formare și forma, iar aceasta, la rândul său, va răspunde în mod clar la întrebarea dacă punctul aparține spațiului de suprafață sau nr.
Metoda cinematică de formare a suprafeței ne conduce la conceptul de determinant, prin care ne referim la un set necesar și suficient de forme geometrice și relațiile dintre ele, care definesc în mod clar suprafața. Condițiile incluse în calificativ ar trebui să includă:
1. O listă de forme geometrice implicate în formarea unei suprafețe.
2. Partea algoritmică, indicând relația dintre aceste cifre.
Astfel, suprafața determinantului este compusă din două părți: dintr-o multitudine de forme geometrice (prima parte) și informații suplimentare cu privire la natura modificărilor formei și care formează dreptul de deplasare (a doua parte). Pentru a distinge prima parte (geometric) determinantului al unei a doua părți (algoritmice), prima condiție este - în runda, iar al doilea - între paranteze drepte; atunci în cazul general, determinantul suprafeței va avea următoarea formă structurală:
unde (T) este partea geometrică, [A] este partea algoritmică.
Trebuie avut în vedere că atunci când specificați o suprafață, în anumite cazuri, în loc de elemente geometrice, puteți specifica parametrii numerici. De exemplu, orice sferă va fi diferită de toate celelalte sfere numai de valoarea razei R, prin urmare, specificând un număr care indică valoarea lui R, definim o singură sferă. Evident, parametrul numeric al suprafeței conice a rotației este ∠φ °, unghiul dintre generatrix și axa suprafeței conice *.
Parametrii de suprafață sunt de două tipuri: parametrii de formă și parametrii de poziție.
Parametrii, modificarea cărora determină o modificare a formei suprafeței, se numește parametrii formei.
Parametrii, care modifică conduc la o schimbare a poziției suprafeței în spațiu, se numesc parametri de poziție.
Suma condițiilor care determină totalitatea tuturor parametrilor independenți ai suprafeței se numește numărul său parametric.
Parametrii formei. În cazurile examinate, parametrul R pentru sferă și ∠φ ° pentru suprafața conică se referă la parametrii formei. Numărul de parametri care modifică forma unei suprafețe poate fi orice număr întreg pozitiv, pornind de la zero. Astfel, de exemplu: numărul de parametri ai formularului pentru plan este zero; pentru o sferă, la una. Dacă suprafața este dată de ecuația ei în formă canonică, toți parametrii formei intră în această ecuație.
Parametrii poziției. Numărul parametrilor care caracterizează poziția suprafeței în spațiu nu poate fi mai mic de trei sau mai mult de șase. De exemplu, pentru un plan este de trei, pentru un elipsoid triaxial este de șase.
Dacă ecuația de suprafață definitorie este făcută într-o poziție arbitrară a suprafeței, acesta conține nu numai că toți parametrii de formă, dar, de asemenea, toate poziția parametri, adică. E. Numărul de parametri independenți ai ecuației în acest caz este egal cu numărul de suprafață parametrice.
Pentru a găsi determinantul unei suprafețe, trebuie să pornim de la modul cinematic al formării sale. Deoarece suprafața poate fi formată în diferite moduri, în mod evident, aceeași suprafață pot avea diferite identificatori, de exemplu, o suprafață de cilindru circular drept (suprafață cilindrică de rotație) pot fi reprezentate cu un punct de vedere cinematic:
a) ca o urmă rămasă în spațiul liniei drepte g în timp ce se rotește în jurul axei i (Figura 117, a); determinantul suprafeței cilindrice de rotație va avea forma
* În ambele cazuri, poziția suprafeței în spațiu nu a fost luată în considerare.
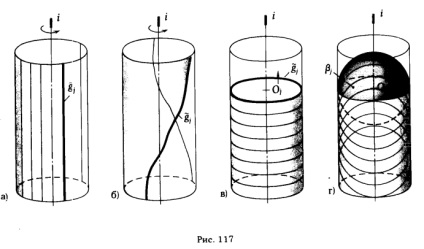
b) ca o urmă de rotație a curbei g. care aparțin suprafeței unui cilindru circular drept, în jurul axei i (Figura 117.6); în acest caz determinantul suprafeței poate fi scris:
c) ca urmare a deplasării translaționale a cercului g. centrul cercului O se mișcă de-a lungul axei i, iar planul său a rămâne în permanență perpendicular pe această axă (Figura 117, c); atunci determinantul suprafeței poate fi scris:
d) ca plicul tuturor pozițiilor suprafeței sferice β, a cărui centru O se deplasează de-a lungul axei i (fig.117, d); În acest caz determinantul ia forma
Din mulțimea determinanților de suprafață, cea mai simplă este de obicei aleasă; în cazul în cauză, un astfel de factor va fi