În dielectrică, viteza luminii EMW depinde de frecvență. Acest fenomen se numește varianță. Efectul dispersiei se manifestă numai în propagarea undelor nonmonocromatice, deoarece componentele sale monocromatice cu frecvențe diferite se propagă la rate diferite. Dispersia este o consecință a dependenței polarizării atomilor de frecvență. Pentru a găsi forma explicită a e (w) care intră în ecuațiile materiale, folosim teoria clasică microscopică a interacțiunii câmpului electromagnetic al valului cu materia. Teoria microscopică provine de la un model idealizat al structurii materiei. Cel mai simplu model este modelul mediu gazos. pentru aceasta, în prima aproximare, se poate ignora interacțiunea dintre atomi sau molecule și se presupune că câmpul care acționează pe un singur atom coincide cu câmpul mediu al EMW. În astfel de condiții, pentru a obține o ecuație de material macroscopic, este suficient să se ia în considerare efectul câmpului EMW asupra unui atom izolat. În general, este necesar să se aplice teoria clasică la astfel de procese cu precauție extremă. Dar în acest caz teoria cuantică a dispersiei conduce la aceleași rezultate ca și teoria clasică.
Teoria clasică a electronului dispersiei interacționează cu câmpul electromagnetic (electron extern sau optic), într-un atom este considerat ca un oscilator dipol amortizat, caracterizat printr-o anumită frecvență naturală a WO și constantă g atenuare, astfel încât ecuația de mișcare în câmpul E (t) = Eo e-iwt a valului de lumină are forma:
unde r este deplasarea electronului din poziția de echilibru. Căutăm o soluție a acestei ecuații sub forma:
Ca rezultat, obținem:
Momentul dipol al atomului p (t), indus de câmpul E (t):
Dacă N este concentrația electronilor cu o frecvență eigenică w0. atunci polarizarea P a mediului se determină după cum urmează:
Pe de altă parte, polarizarea mediului (polarizarea mediului) este
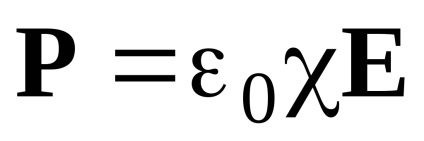
unde c este susceptibilitatea dielectrică liniară a mediului. care în general depinde de frecvența w. De asemenea, luăm în considerare faptul că vectorii D. E și P sunt legați de relația:
Apoi rezultă din (4.10) și (4.11) că pentru permeabilitatea relativă :, (4.12)
și din (4.8), (4.9), (4.10) avem:
pentru că
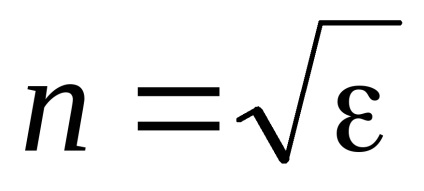
Apoi, ținând seama de (4.14), avem ecuațiile:
G este foarte mic pentru dielectrice transparente sau parțial transparente în domeniul optic. atunci
Din această aproximație obținem:
Dacă în mediu dispersia este determinată de diferite ansambluri de electroni cu frecvențe proprii w0i și concentrație de Ni. atunci formula (4.18) poate fi generalizată:
Această formulă nu ia în considerare vibrațiile ionilor. pentru că masa lor este mult mai mare decât masa electronilor, atunci frecvențele naturale ale ionilor se află în regiunea infraroșie îndepărtată.
9 Dispersie normală. Departe de propriile rezonanțe, magnitudinea
D
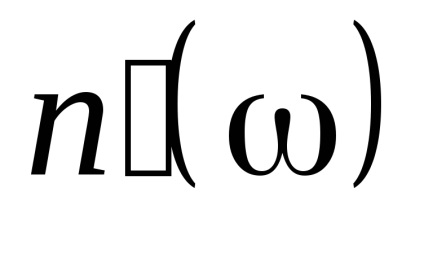
Dacă partea reală a indicelui de refracție crește cu frecvență în creștere, atunci dispersia se numește normal. Dispersia normală este observată în toată regiunea de transparență a dielectricilor. Pentru frecvențe mici (w < Această valoare poate diferi semnificativ de valoarea indexului de refracție pentru frecvențele optice. (De exemplu, pentru apă în domeniul de frecvență optic n = 1,33 și valoarea statică 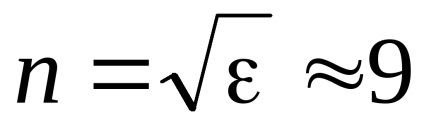
Pentru frecvențe mari (w >> w0i), în acest caz
astfel pentru radiații de undă scurtă, un izolator este un mediu optic mai puțin dens decât un vid. De exemplu, pentru raze X, se poate observa o reflecție completă. În plus, la frecvențe foarte înalte, natura legării electronilor nu joacă un rol, iar indicele de refracție n depinde numai de concentrația totală a tuturor electronilor.
Dispersia anomală. Neglijarea amortizării (g = 0) a dus la faptul că
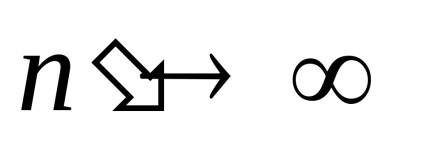
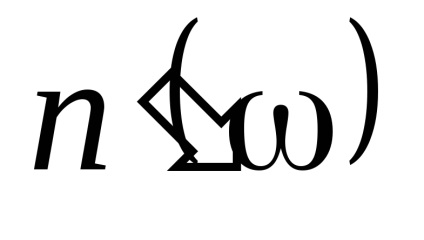
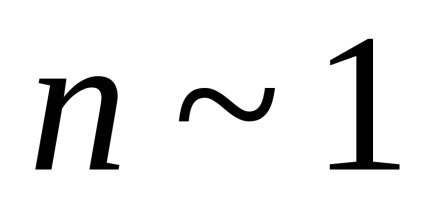
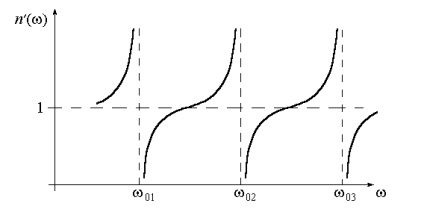
Curbele de dispersie (4.24) sunt prezentate în figura 4.2.
Lângă frecvența de rezonanță w0, indicele de refracție
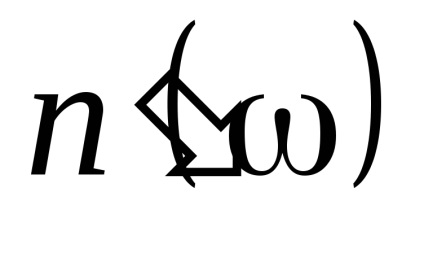
fenomenul se numește o dispersie anormală.