B10 (nivel ridicat, timp - 10 min)
Tema. Transformarea expresiilor logice.
Ce trebuie să știți:
simboluri convenționale ale operațiilor logice
A echivalență ↔ B (echivalență, echivalență)
tabele de adevăr ale operațiilor logice "AND", "OR", "NOT", "implicare", "echivalență" (vezi prezentarea "Logică")
operația "implicație" poate fi exprimată prin "OR" și "NOT":
operațiunea "echivalență" poate fi exprimată și prin "OR" și "NOT":
dacă nu există paranteze în expresie, mai întâi se fac toate operațiile "NOT", apoi - "AND", apoi - "OR", iar ultima - "implicație"
produsul logic A ∙ B ∙ C ∙ ... este egal cu 1 (expresia este adevărată) numai atunci când toți factorii sunt egali cu 1 (și în restul cazurilor este 0)
suma logică A + B + C + ... este 0 (expresia este falsă) numai atunci când toți termenii sunt 0 (și în alte cazuri este 1)
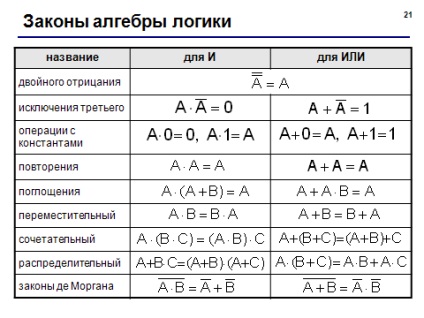
reguli pentru conversia expresiilor logice (slide din prezentarea Logic):
Exemplu de sarcină:
Care este cel mai mare număr întreg X pentru care afirmația adevărului este adevărată
Soluție (opțiunea 1):
Este o operație de implicare între două relații și
încercați mai întâi să rezolvați inegalitățile
desemnează aceste regiuni pe axa X:
În figură, zonele violete denotă regiunea în care expresia este adevărată, zona albastră este aria în care este adevărată
amintiți tabelul de adevăr al operației "implicații":
Soluție (în întregi):
este o operație de implicare între două relații:
desigur, aici puteți aplica aceeași metodă ca în exemplul precedent, dar va trebui să rezolvați ecuații patratice (nu doriți să ...)
rețineți că, prin condiție, suntem interesați doar de numere întregi, astfel încât să puteți încerca cumva să transformați expresia originală, obținând o declarație echivalentă (după cum reiese din exemplul anterior, valorile exacte ale rădăcinilor nu ne interesează deloc!)
să luăm în considerare inegalitatea: este evident că poate exista atât un număr pozitiv, cât și un număr negativ;
este ușor de verificat că, în domeniu, afirmația este adevărată pentru toate numerele întregi și în domeniul pentru toate numerele întregi (pentru a nu se confunda, este mai convenabil să se utilizeze inegalitățile non-stricte u, în loc de u)
Prin urmare, pentru numere întregi poate fi înlocuită cu o expresie echivalentă
domeniul adevărului expresiei este unirea a două intervale infinite:
Luați în considerare a doua inegalitate: este evident că pot exista și numere pozitive și negative;
în regiune afirmația este valabilă pentru toate numerele întregi și în domeniul pentru toate numerele întregi, prin urmare, pentru întregi se poate înlocui cu o expresie echivalentă
Domeniul adevărului expresiei este un interval închis, marcat de o bandă albastră
amintiți tabelul de adevăr al operației "implicații":
conform tabelului, expresia dată este valabilă peste tot, cu excepția regiunilor unde u; Aria adevărului este evidențiată în verde în figură;
Rețineți că valoarea nu mai intră în zona verde, deoarece acolo și, adică implicația, dă 0
conform schemei este clar că întregul maxim în zona verde este 2
astfel, răspunsul corect este 2.
trebuie să ne amintim că luăm în considerare valoarea expresiei numai în ansamblu, în același timp, există particularitățile sale proprii: poate fi tentat să extindă zona verde la punctul în care va conduce la un răspuns greșit, pentru că există deja
Un alt exemplu al sarcinii:
Câte soluții diferite face ecuația
unde K, L, M, N sunt variabile logice? Răspunsul nu trebuie să enumere toate seturile diferite de valori ale lui K, L, M și N pentru care este menținută egalitatea dată. Ca răspuns, trebuie să specificați numărul de astfel de seturi.
Soluție (opțiunea 1, împărțire în părți):
Rescrim ecuația folosind mai multe simboluri simple pentru operații:
din tabelul de adevăr al operației "implicare" (a se vedea prima problemă) rezultă că această egalitate este adevărată dacă și numai dacă simultan
din prima ecuație rezultă că cel puțin una dintre variabilele K sau L este 1 (sau ambele); deci luați în considerare trei cazuri
dacă K = 1 și L = 0, atunci a doua egalitate este valabilă pentru orice M și N; Deoarece există 4 combinații de două variabile logice (00, 01, 10 și 11), avem 4 soluții diferite
dacă K = 1 și L = 1, atunci a doua egalitate este valabilă pentru M · N = 0; există 3 astfel de combinații (00, 01 și 10), avem 3 soluții suplimentare
dacă K = 0, atunci L = 1 (din prima ecuație); a doua egalitate este valabilă pentru M · N = 0; există 3 astfel de combinații (00, 01 și 10), avem 3 soluții suplimentare
Astfel, în total, obținem 4 + 3 + 3 = 10 soluții.