Pentru a descrie suprafața pământului într-un avion este să descrieți contururile diferitelor obiecte de teren de pe acesta. Fiecare contur este o serie continuă de puncte. Imaginea suprafeței pământului pe plan este astfel redusă la imaginea punctelor individuale.
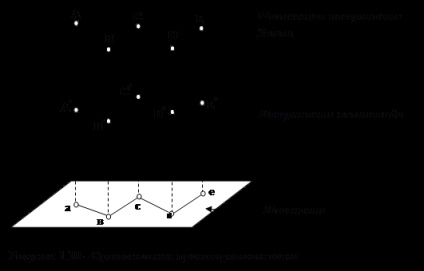
Când imaginile diferitelor contururi ale suprafeței pământului sunt desenate pe un plan (hârtie), toate punctele lor sunt proiectate dintr-o suprafață fizică complexă a Pământului pe o suprafață mai simplă de-a lungul perpendicularilor pe această suprafață (Figura 1.10). Aceste suprafețe pot fi suprafața elipsoidului, a mingii sau a planului pământului.
Proiectarea punctelor de pe suprafața pământului de-a lungul perpendicularilor pe suprafața acceptată se numește proiecție rtogonală.
Atunci când se prezintă suprafețe mici pe teren (pe plan), curbura suprafeței pământului este neglijată, adică o secțiune de teren este luată drept avion. Care ar trebui să fie dimensiunea unor astfel de zone, astfel încât curbura lor să poată fi neglijată?
Luăm figura Pământului pentru o sferă de rază R (Figura 1.11). Fie AB = S distanța pe minge, fie unghiul central corespunzător arcului S. Desenați planul tangent la punctul A și extindeți raza OB la intersecția cu acest plan în punctul C.
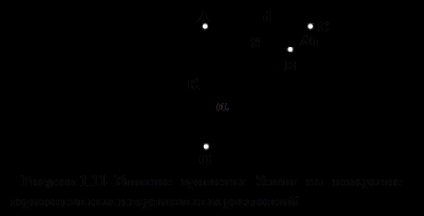
Dacă secțiunea sferei S este luată drept planul corespunzător segmentului tangent AC = d. atunci vom avea o eroare la distanța orizontală
dar în verticale
Figura 1.11 arată că
unde unghiul este exprimat în radiani. atunci
Se știe că tg = + 1/3 3 + 2/15 5 +.
Limitându-ne la primii doi termeni ai acestei serii descrescătoare, și neglijând pe cele ulterioare, având în vedere micuța lor, obținem
Având în vedere că = S / R, obținem
d = d 3/3 R 2 (1.7)
Presupunând că R = 6371 km, d = 10 km, obținem d / d = 1/1000000. O astfel de eroare este considerată admisibilă cu cele mai exacte măsurători pe suprafața pământului. Prin urmare, dacă partea de suprafață a pământului descrisă pe plan nu depășește un cerc cu un diametru de 20 km, atunci partea corespunzătoare a suprafeței plane poate fi considerată drept plan. Cu distanța de creștere d, eroarea d crește rapid, deoarece este proporțională cu cubul distanței.
Acum determinăm magnitudinea erorii h în distanța verticală datorită ne-calculului curburii Pământului.
Din triunghiul OAC ajungem
R2 + d2 = (R + h) 2 = h (2R + h) + R2 (1,8)
Substituind în formula (1.2) diferite valori ale lui d, obținem următoarele erori h:
d, km. 0,10 1,0 2,0 3,0 10,0
h, vezi 0,08 7,8 31 71 785
Cu lucrarea geodezică inginerică, precizia cerută a marcajului este caracterizată de erori mai mici de 1-2 cm, astfel încât influența curburii Pământului asupra determinării altitudinilor ar trebui, de regulă, luată în considerare.
Întrebări pentru control
1. Probleme de geodezie inginerie
2. Idei contemporane despre figura Pământului
3. Sistemul coordonatelor geografice
4. Sistem de coordonate dreptunghiulare și polare
5. Esența proieciei lui K. Gauss
6. Ce înseamnă coordonatele punctului X = 5345123 m? Y = 12345678 m?
7. Conceptul de înălțime absolută, relativă a punctelor.
8. Cum se proiectează suprafețele fizice ale pământului pe un plan elipsoidic?
9. Cum se calculează eroarea în distanța măsurată atunci când nu este luată în considerare curbura Pământului?
10. Cum se calculează eroarea în altitudinea măsurată datorită ne-calculului curburii Pământului?