Sarcinile de trigonometrie fac parte integrantă din orice examen serios. O pregătire rară pentru USE în matematică nu costă atenția tutorelui la această secțiune voluminoasă și complexă. Acesta este asociat cu cel mai mare număr de greșeli de eroare privind UTI în rândul celor slab intrați. Să luăm în considerare particularitățile metodologice ale studierii trigonometriei și a tehnicilor private, pe care le folosește de obicei tutorele din matematică. Voi face câteva pagini pe această temă. La început, să vorbim despre introducerea unui cerc trigonometric.
Din păcate, standardele GIA privind matematica au fost nevoite să revizuiască programa școlară, în care s-au făcut schimbări semnificative în acest an. În mod tradițional, trigonometria studiată în clasa 9 a fost înlocuită de statistici și de teoria probabilităților. Tutoring matematica aceasta complica doar munca. Desigur, chiar înainte de examenul de atestat algebră nu a afectat sines și cosines, dar cel puțin introducerea în trigonometrie a fost studiată. Acum totul sa schimbat la rădăcină, iar "startul" trebuie luat în clasa a 10-a. Pentru un tutore, aceasta înseamnă combinarea pregătirii de doi ani pentru UTI cu învățarea de a lucra pe cercul trigonometric de la zero. Dar nu este nimic de făcut, este necesar să se adapteze noilor standarde și manuale. Deci, ce metode metodice oferă tutorelui matematic în acest subiect? Cât de diferită este abordarea introducerii cercului? Cum de a construi un loc de muncă cu un student slab?
Studiul trigonometriei începe cu măsurarea și amânarea unghiurilor. Și deja în acest stadiu, profesorul de matematică se poate confrunta cu anumite probleme. Cu ce sunt legate? De obicei, acestea confundă locația colțurilor pe cerc și nu o văd în "stare deschisă". În nici un manual nu am întâlnit încă ceea ce spun elevilor mei. Să ne uităm la desenul cercului. Ce este? În ochii elevului, aceasta este o linie închisă limitată, pe care tutorele de matematică lovește câteva cifre și litere, anunțându-le cu colțuri. Despre același punct sunt semnate simultan câteva valori diferite. Ce este asta? Și radiani în loc de gradele obișnuite. Confuzia apare teribilă. Mai ales atunci când un profesor în matematică merge la soluția de ecuații trigonometrice simplu (aceasta este un subiect în manualul Mordkovich este aproape direct în spatele cercului trigonometrice). Cum să clarificați ce se întâmplă?
Tehnica spirală a matematicii
Întotdeauna mișc cercul trigonometric. Cum? Ce este această acțiune? Este foarte simplu. Eu explic acest lucru: "Unghiurile, ca și lungimile segmentelor, sunt reprezentate grafic pe o axă infinită. Numai pentru lucrul practic cu procesul de imagine este mai convenabil să înfășurați această axă cu bucle sau, cu alte cuvinte, să o reprezentați sub forma unei spirale ". Și arăt imaginea:
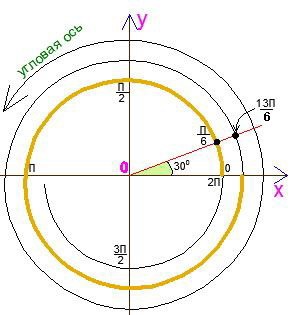
Cu această abordare, profesorul de matematică oferă o transparență deplină a acțiunilor cu colțuri și claritate în imaginea lor. Pentru a simplifica lucrul elevului cu cercul, este necesar să-l dăm ca o axă pentru colțuri, care, ca o frânghie, a fost înfășurată pe o țeavă și a atras profilul rezultat. Această tehnică îi ajută pe tutorele din matematică să elimine un număr mare de probleme nu numai la etapa de introducere a cercului, ci și în lecțiile ulterioare. în special în rezolvarea ecuațiilor și inegalităților, atunci când trebuie să notăm o întreagă serie de unghiuri, reprezentate de același punct sau arce suprapuse unul pe celălalt. Îi sfătuiesc pe tutore să selecteze o parte a cercului care corespunde unei singure virajuri (în figură este afișată în culoarea brună) și să o numească o "cale".
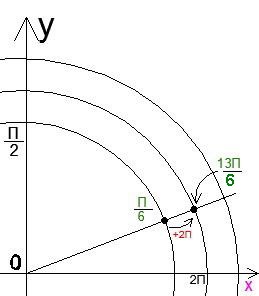
Elevul trebuie să învețe că imaginea manualului este o imagine a unei spirale strânse, ca și cum tubul era înfășurat strâns cu o frânghie. În acest caz, diferite semne (diviziuni) ale axei (adică frânghii) vor fi suprapuse unul pe altul și vom vedea că semnele de unghiuri diferite se îmbină într-un singur punct. Dacă slăbim frânghia, obținem o spiră pe care fiecare colț este reprezentat separat.
În momentele în care profesorul de matematică simte neînțelegere și confuzie cu colțurile, imaginea cercului într-o formă spirală vine la salvare. De exemplu, soluția ecuației trigonometrice poate fi prezentată după cum urmează:
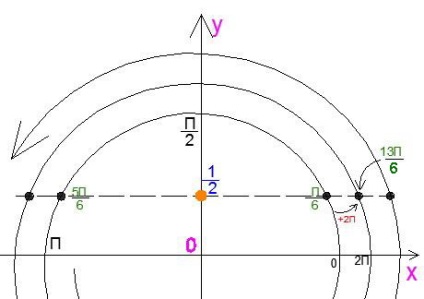
Trebuie spus că punctele negre (unghiurile) sunt soluția ecuației. Și dacă strângem spirala (strângeți frânghia pe țeava), atunci ei se vor strânge unul pe altul și se vor transforma în stânga și la dreapta. După aceea, tutorele poate face un desen standard. În acest fel va fi mai ușor pentru profesor să explice formulele și. iar studentul își va aminti mai bine natura periodică a locației rădăcinilor.
Alexander Nikolaevich, profesor de matematică din Moscova, stația de metrou Strogino