Bună ziua, dragi studenți ai Universității Argemon! Mă bucur să vă văd la următoarea conferință despre magia funcțiilor și integralelor.
Astăzi avem pe ordinea de zi - studiind, în primul rând, magia parabolei. Vom începe cu asta.
Vedere generală a parabolei (funcția patratică)
Coeficienții b și c pot fi zero (simultan sau nu), dar coeficientul "a" nu poate fi egal cu zero, altfel nu va fi o funcție patratică.
Cea mai simplă funcție parabolă are forma
Vedem că această funcție nu are singularități. Prin urmare, domeniul de definiție este întreaga linie de număr (-∞; + ∞), iar mulțimea de valori este doar partea non-negativă a liniei drepte [0; + ∞).
Și acum, folosind cunoștințele obținute în lecțiile anterioare, încercați să utilizați coeficienții magicieni pentru a schimba magia funcției.
Adăugarea coeficientului "a", altul decât 1, duce la o schimbare în intervalul ramurilor parabolei. Dacă | a |> 1, parabola devine mai îngustă și dacă | a |<1, то ветви расходятся в стороны и парабола становится шире.
Acum, ia în considerare această funcție
Adăugarea constantului "c" ca termen al expresiei cu un pătrat duce la mutarea parabolei în sus sau în jos în pozițiile "c". În consecință, setul de valori ale funcției se modifică.
Acum, puteți ghici că adăugarea termenului bx, evident, va duce la deplasarea parabolului orizontal.
Să examinăm acest aspect mai detaliat. Să încercăm să selectăm un pătrat complet în expresie (1). De fapt, atunci când există coeficienți numerici în ecuație, totul este mult mai clar, deci trecem de la coeficienții literei la coeficienții numerici:
a = 2; b = 4; c = 5
y = 2 x 2 + 4x + 5 = 2 (x + 1) 2 + 3
Acum începeți cu atenție dezasamblarea magiei acestei funcții patrate. Să începem din interior.
Vedem că în pătrat nu x, a (x + 1). Din lecțiile anterioare, ne amintim că termenul de coeficient de lângă x provoacă magia mutării funcției orizontal spre dreapta sau spre stânga. În cazul nostru, 1 unitate la stânga.
Apoi, acordați atenție coeficientului de 2 în jurul pătratului. Aceasta va provoca magia compresiei parabolice. Va fi deja. Dacă acest coeficient ar fi de asemenea negativ, parabola s-ar transforma la 180 de grade, iar ramurile ar privi în jos.
Apoi, coeficientul 3 intră în joc și aplică magia lui, determinând parabola să se deplaseze cu 3 unități în sus.
Sarcina 1. Orice își ia parabola (1).
Coeficienții sunt definiți după cum urmează:
a = primul număr din numărul LD
b = al doilea număr din numărul LD
c = al treilea număr din numărul dvs. LD sau a-b, dacă numărul dvs. LD este format din două cifre.
Este necesar să investigăm această parabolă în același mod ca și în lecție, notând și intervalele de scădere și creștere.
Lecția nu sa terminat încă. Să mergem mai departe. Poziția parabolului în axele de coordonate depinde de coeficienții a, b, c.
Din semnul coeficientului a depinde modul în care se îndreaptă ramurile parabolei:
Dacă a> 0, atunci ramurile parabolei sunt îndreptate în sus;
dacă a<0, то ветви параболы направлены вниз.
Cred că îți amintești cum sunt căutate rădăcinile ecuației patratice care corespund unei funcții patrate,
Da, da, prin calculul discriminantului. Rădăcinile pot fi 2, poate una (de fapt, rădăcinile 2, dar ele sunt aceleași) sau să nu fie rădăcini. Dar nu există rădăcini reale, dar există rădăcini virtuale, dar nu vom vorbi încă despre astfel de rădăcini, deși dezvăluie o magie mai interesantă, dar mai mult despre aceasta mai târziu. mult mai târziu. Dacă sunteți interesat de acest lucru, atunci vom reveni la rădăcinile imaginare și la magia funcției variabilei complexe. Și magia ei este chiar mai uimitoare și poate crea minuni pe care mulți nu le-au visat niciodată. Dar, pentru moment, vom vorbi doar despre rădăcinile reale ale ecuației patratice.
Deci, dacă rădăcinile sunt 2, atunci aceasta înseamnă că parabola intersectează axa OX la două puncte.
Dacă rădăcina este una (sau mai degrabă, două identice), atunci înseamnă că parabola atinge axa OX la un punct.
Dacă, totuși, discriminantul ecuației patratice corespunzătoare funcției patratice este negativ, întreaga parabolă este fie deasupra axei OX, fie sub ea.
Încă o dată, aș vrea să vă atrag atenția asupra faptului că zona definiției parabolice este întreaga axă numerică, dar setul de valori depinde de poziția parabolei.
Sarcina 2. În graficele de mai sus, numărarea scalei de 1: 1, specificați setul de valori ale tuturor funcțiilor 1-6.
Și acum ne vom familiariza repede cu forma generală a funcției de putere
y = xn. n este un număr natural (4)
Este clar că atunci când n este un număr par, atunci forma funcției este similară cu (1).
Dacă n este un număr impar, atunci graficul funcției încetează să fie uniform, devine ciudat și condiția f (-x) = -f (x) este satisfăcută. Acest tip de funcție se numește de asemenea o parabolă cubică.
Sarcina 3. Găsiți domeniul de definiție și setul de valori pentru funcția (4) pentru diferite n (par și impar).
Și, în sfârșit, ultimul. Considerăm funcția inversă funcției (4). Care este operația inversă a exponentierii? Desigur, extragerea rădăcinii.
Și aici trebuie luate în considerare două cazuri.
1. n-nici. Domeniul de definiție este semiaxisul negativ [0; + ∞), deoarece o rădăcină de grad egal nu poate fi extrasă dintr-un număr negativ.
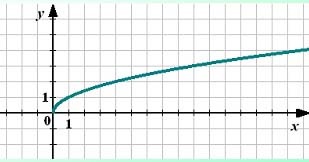
2. n este un număr impar. Graficul are următoarea formă
Sarcina 4. Specificați zona de definiție și setul de valori pentru funcție (5). Comparați graficele funcțiilor (4) și (5).
Și în final vă voi arăta cum sunt construite graficele funcțiilor inverse. Graficele funcțiilor inverse sunt simetrice în raport cu bisectorul 1 și 3 ale unghiurilor de coordonate. Prin urmare, este suficientă trasarea acestei linii și oglindirea graficului funcției de putere în mod simetric față de ea.
În figură am prezentat ambele cazuri de funcții de putere și inverse. După cum vedem, în cazul n-odd, totul este bine: ambele ramuri sunt reflectate simetric de către bisector și se obține o funcție. Dar în cazul lui n-even, una dintre ramuri este punctată, deoarece nu intră în graficul funcției, deoarece curba obținută prin reflexia simetrică nu va fi o funcție.
Sarcina 5. Arătați că dacă includeți linia punctată în grafic, atunci acesta va fi deja un grafic al funcției.
Trimiteți lucrarea prin Biroul personal
Puteți să vă transferați în siguranță întrebările cu Persephone
Cea mai bună ofertă în salonul jaguar xj de la distribuitorul oficial.