Într-un cristal, toate nivelurile de energie pot fi împărțite în trei benzi energetice. Nivelele de energie ale electronilor de valență de atomi formează o bandă de valență (vezi figura 3). Electronii liberi pot avea în cristal nu orice, ci anumite valori discrete (unele definite) ale energiei. Nivelele de energie ale electronilor liberi formează o zonă liberă sau o bandă de conducere.
Zona liberă este separată de banda de valență de o bandă interzisă - o bandă de energie interzisă de electroni. Cantitatea DE se numește lățimea benzii interzise.
La o temperatură, electronii cristalului umple nivelele mai scăzute de energie. Conform principiului lui Pauli. la fiecare nivel de energie nu pot exista mai mult de doi electroni cu rotiri îndreptate opus.
În semiconductori la o temperatură de 0 K, banda de valență este complet umplută de electroni. Nu există electroni în zona liberă. Lățimea benzii interzise a semiconductorilor este mică: de ordinul a 1 eV. Cu o temperatură în creștere, electronii, obținând energie, pot trece la niveluri mai ridicate de energie. Energia mișcării termice a electronilor și energia câmpului electric al curentului este suficientă pentru trecerea electronilor de la banda de valență a semiconductorului la banda de conducție.
Când un semiconductor este conectat la o sursă de curent, în circuit apare un câmp electric. Electronii liberi din banda de conducere sub acțiunea acestui câmp se deplasează opus câmpului (vectorul de intensitate a câmpului electric) și formează conductivitatea electronică a semiconductorului. În banda de valență, la locul electronului stâng rămâne o sarcină electrică pozitivă necompensată - o gaură. Sub acțiunea unui câmp electric, un electron de la un nivel adiacent poate ajunge la locul găurii, unde electronul a lăsat o nouă gaură formată. Putem spune că găurile se mișcă de-a lungul câmpului. Gaurile din banda de valență formează conductivitatea semiconductorului. Conductivitățile electronice și ale găurilor unui semiconductor chimic pur formează conductivitatea intrinsecă a unui semiconductor.
Conductivitatea electrică într-un cristal este proporțională cu concentrația purtătoarelor de curent (electroni și găuri). Distribuția electronilor peste nivelele de energie se caracterizează prin funcția Fermi-Dirac
unde E - electroni de energie, EF - energia Fermi, k = 1,38 # 8729; 10 -23 J / K - constanta Boltzmann T - temperatura absolută a cristalului.
Este funcția Fermi-Dirac. care determină probabilitatea de a găsi un electron la un nivel de energie cu o energie E.
At = 1 la nivelul energiei există 2 electroni;
= 0,5 la nivelul energiei există un electron;
= 0 nu există nici un electron la nivelul energiei.
Într-un metal, energia Fermi este energia cinetică maximă pe care electronii de conducere o poate avea la o temperatură de 0 K. Nivelul de energie corespunzător energiei Fermi se numește nivelul Fermi. Astfel, nivelul Fermi este nivelul de energie superior umplut cu electroni într-un metal la o temperatură de 0 K.
Valoarea nivelului Fermi într-un semiconductor chimic pur, măsurată de la vârful benzii de valență, este aproximativ egală cu jumătate din lățimea benzii interzise
Rezultă că nivelul lui Fermi se află în mijlocul zonei interzise. Dacă energia electronului din banda de conducție este E. apoi din figura 3 se poate observa că
La temperaturile scăzute din formula (1), unitatea din numitor poate fi neglijată. Luând în considerare expresia (3), formula (1) se obține
Conductivitatea specifică a unui semiconductor este proporțională cu concentrația purtătoarelor actuale și, prin urmare, este proporțională cu funcția Fermi-Dirac (formula (4)), atunci putem scrie
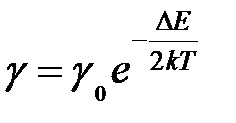
unde este o constantă în funcție de semiconductorul dat. Rezistența este invers proporțională cu conductivitatea, astfel încât poate fi reprezentată în formă
Aici A este un coeficient care depinde de proprietățile fizice ale semiconductorului. Se poate observa din formula (5) că rezistența semiconductorului R scade odată cu creșterea temperaturii. Conform teoriei, acest model de bandă este explicată după cum urmează: o creștere a temperaturii mărește numărul de electroni în zona liberă și numărul de găuri în banda de valență, prin urmare, conductivitatea semiconductorului este crescută, iar rezistența scade. În cazul metalelor, rezistența crește odată cu creșterea temperaturii.
Pentru a determina lățimea decalajului de bandă, este necesar să se ia formula logaritmică (5)
Coeficientul A este necunoscut, deci scrieți mai întâi formula (6) pentru două temperaturi diferite T1 și T2
Expresia (8) este scăzută din formula (7)
Din formula (9) pentru lățimea decalajului benzii, formula calculată
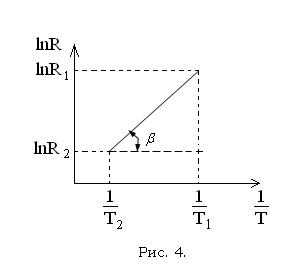
Comparând formulele (10) și (11), se poate obține
Coeficientul de temperatură de rezistență arată schimbarea relativă a rezistenței atunci când substanța este încălzită cu 1 K
Unitate de măsură în SI.
Luând derivatul rezistenței la temperatură în formula (5), putem scrie:
Formula (13) este substituită în formula (12) și luând în considerare formula de rezistență R (5), obținem
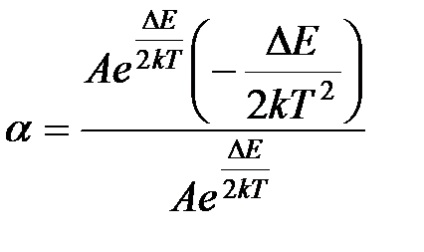
Formula de calcul pentru coeficientul de temperatură de rezistență al unui semiconductor este
Coeficientul de temperatură al rezistenței semiconductoarelor depinde de temperatura și natura chimică a substanței. Formula minus în formula (14) ia în considerare faptul că, cu creșterea temperaturii, rezistența semiconductorului scade. În metale, coeficientul de temperatură de rezistență este o valoare pozitivă.
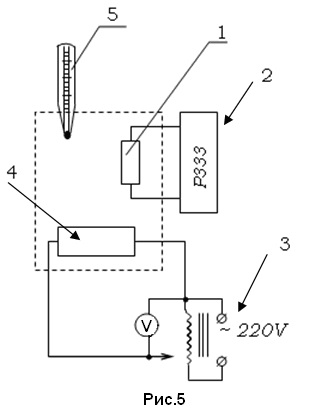
Figura 5 prezintă o diagramă a unei instalații de laborator. Termostatul 1, termometrul 5 și încălzitorul 4 sunt plasate într-un vas închis.
Tensiunea la încălzire este furnizată de la un transformator (LATR) conectat la rețea 3. Un termistor este un semiconductor a cărui rezistență este dependentă de temperatură. Rezistența este măsurată printr-o punte de tip P333.
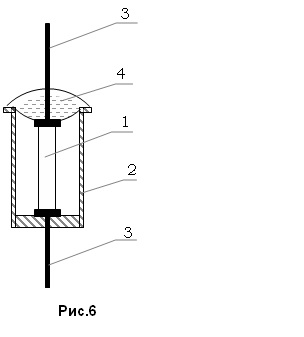
Pentru cercetare, se utilizează un termistor OSMMT-4 (figura 6), constând dintr-un amestec de oxizi de cupru și mangan. Termostatul 1 sub forma unei tije este într-o carcasă metalică închisă 2. Terminalele 3 sunt etanșate cu un strat de staniu și un izolator de sticlă 4.
Termorezistorii sunt utilizați pentru măsurarea temperaturii.
1. Rezistența termistorului la temperatura camerei este măsurată prin intermediul punții 2.
2. Porniți încălzitorul.
3. Măsurați rezistența termistorului la fiecare C.
Efectuați 4 - 5 măsurători, fără a permite o creștere a temperaturii mai mare decât C.
4. Înregistrați rezultatele măsurătorilor în Tabelul 1.
5. Construiește un grafic al rezistenței față de temperatură în coordonatele lnR și T.
6. Calculați valoarea energiei de activare (lățimea intervalului de bandă) cu formula (10).
7. Calculați coeficientul de temperatură de rezistență al semiconductorului cu formula (14).
8. Înregistrați rezultatele calculelor și trageți o concluzie.
6. Întrebări de testare
1. Cum apare divizarea nivelurilor de energie în zonele dintr-un solid cristalin?
2. Cum se formează forma de valență?
3. Cum se formează banda de conducție (zonă liberă)?
4. Cum apare conductivitatea intrinsecă a semiconductorilor?
5. Ce lege respectă distribuția electronilor asupra nivelurilor energetice?
6. Care este semnificația fizică a funcției Fermi-Dirac?
7. Cum se schimbă rezistența unui semiconductor cu creșterea temperaturii? (Construiește un grafic al acestei funcții). Comparați cu metalele.
8. Care este coeficientul de temperatură de rezistență? Care este dependența de temperatură? Comparați coeficientul de temperatură pentru rezistența semiconductorilor și a metalelor.
Lucrul B-6. Studiul proprietăților joncțiunii p-n și îndepărtarea caracteristicilor statice ale tranzistorului
Pentru a studia funcționarea unei diode semiconductoare și a unui tranzistor. Urmăriți modificarea curentă prin intersecția p-n, în funcție de variația de tensiune în direcțiile înainte și oprită. Îndepărtați caracteristicile statice ale tranzistorului.