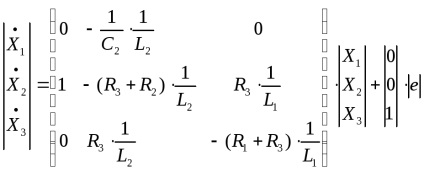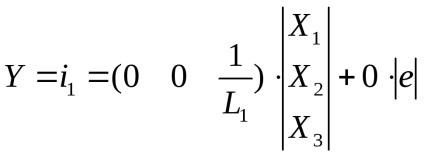Filtrul de formare este un sistem staționar liniar, care la semnalul de intrare, sub formă de zgomot alb, formează la ieșire un proces aleator X (t) cu caracteristici statistice date.
Pentru a determina funcția de transfer a filtrului de formare, folosim ecuația (17):
.
shot
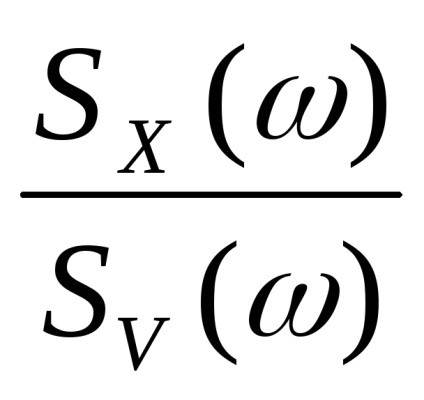
Astfel, pătratul modulului răspunsului de frecvență poate fi reprezentat în forma:
,
unde
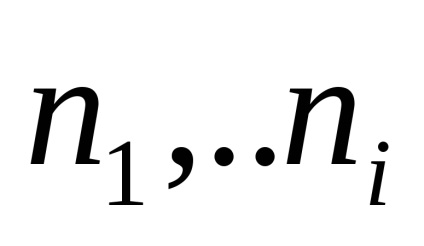
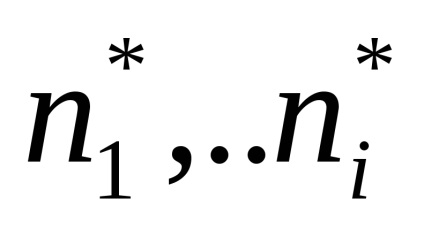

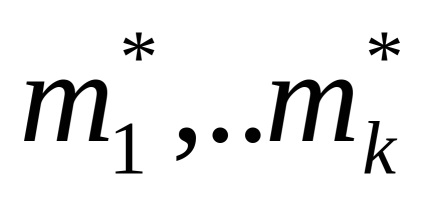
Constatând că rădăcinile sunt pereche complexe-conjugate (adică
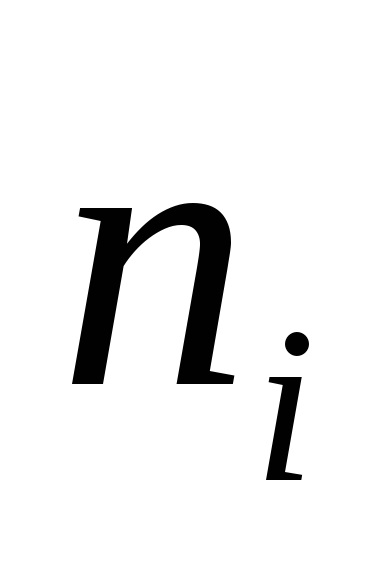
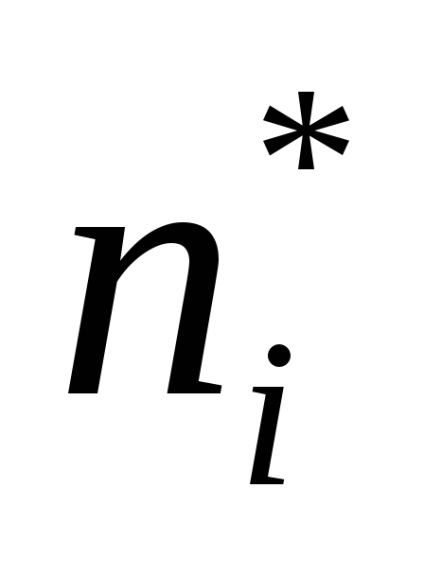
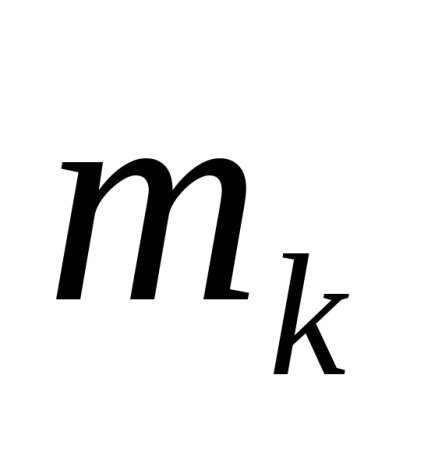
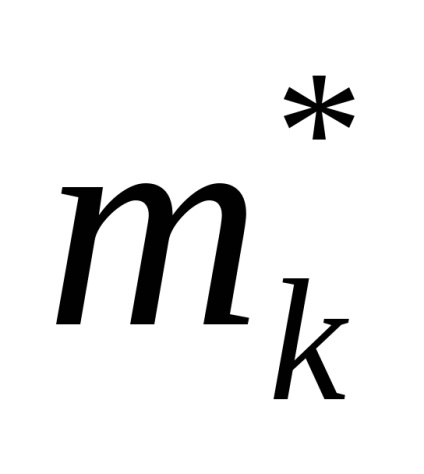
,
.
Astfel, pentru a forma expresia funcției de transfer a filtrului de modelare
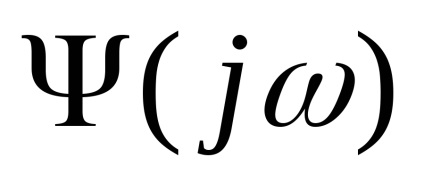
Funcția de corelare, densitatea spectrală a procesului staționar, caracteristicile zgomotului alb
Un proces staționar este un proces aleatoriu care nu-și schimbă caracteristicile în timp și toate funcțiile n-dimensionale de distribuție a probabilităților nu se modifică în funcție de schimbarea originii timpului.
Funcția de corelare staționară este o funcție aleatorie cu așteptări matematice constante și un coeficient de corelație care depinde de diferența dintre argumente.
.
Densitatea spectrală a unui proces aleatoriu staționar X (t) este o funcție de frecvență care caracterizează compoziția spectrală a procesului și este determinată de expresia:
Relația dintre densitatea spectrală și funcția de corelare:
.
Zgomotul alb este un proces aleatoriu staționar care are o densitate spectrală constantă.
.
Un proces aleator cum ar fi zgomotul alb are întotdeauna o legătură între implementările anterioare și cele ulterioare. În acest sens, funcția de corelare a zgomotului alb are forma:
.
Funcția de corelație a zgomotului alb cu o precizie pentru const este o funcție δ - un impuls:
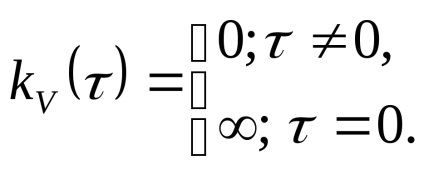
Zgomotul alb este un proces aleator staționar a cărui secțiune transversală este variabile aleatoare necorrelate cu variante infinite:
.
Distingeți intensitatea zgomotului alb, în acest caz este considerat un proces aleator non-staționar:
,
unde
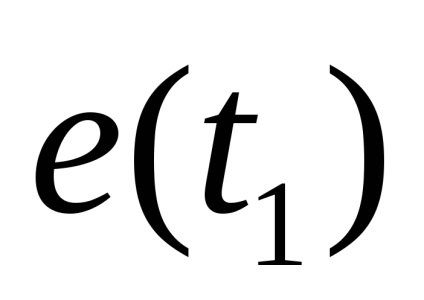
Construirea unui model matematic pentru circuitul electric
Să considerăm un exemplu de construire a unui model matematic în spațiul de stare pentru un obiect de control reprezentat sub forma unui circuit electric (Figura 3)
Figura 3. Diagrama electrică a obiectului de control
Obiectul de control este specificat sub forma unui circuit electric și pentru trecerea la o descriere matematică a obiectului, este necesar să se noteze ecuațiile pentru toate circuitele prin a doua lege a lui Kirchhoff. Și pentru a găsi un sistem de ecuații care descriu obiectul de control prin metoda curenților de contur. Curentul de ieșire este curentul în circuitul primar i1.
Pentru tranziția la descrierea matematică a obiectului, scriem ecuațiile pentru toate buclele conform celei de-a doua lege a lui Kirchhoff și găsim un sistem de ecuații care descriu obiectul de control prin metoda curenților de contur. În cazul nostru:
În sistemul inițial de ecuații, trebuie să scăpăm de toate integralele, diferențiind ecuațiile.
Scapa de integrale în ultima ecuație:
Folosind metoda integrării condiționale, este necesar să se introducă variabile fictive egale cu elementele luate din ecuații, dar cu 1 sau mai multe ordine de mărime mai mici.
În cazul nostru, folosind metoda integrării condiționale, introducem variabile fictive egale cu elementele luate din ecuația (22) cu 1 și 2 ordine de mărime mai mici și de la prima ecuație a sistemului (21).
Derivații în raport cu timpul din variabilele fictive se găsesc și, aplicând ecuațiile anterioare, sunt exprimate prin dependența curenților și a variabilelor fictive.
Pentru acest caz:
Din sistemul (23) (și dacă este necesar (21)), curenții sunt exprimați astfel încât să depindă numai de variabilele manechinului.
Din sistemul (23), expresiile pentru curenți prin variabilele manechine pot fi scrise sub forma:
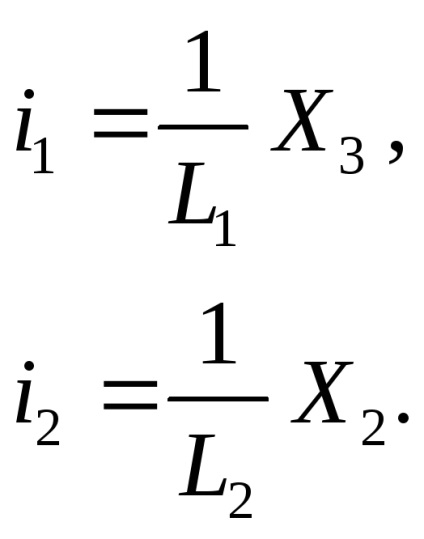
Expresiile curente rezultate sunt înlocuite în sistem (24), iar sistemul este suplimentat cu o expresie pentru cantitatea de ieșire, ca rezultat, este obținut.
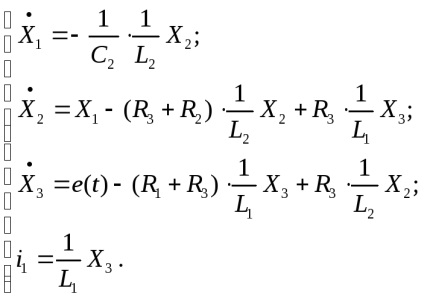
Pe baza sistemului de ecuații obținut și a ecuației pentru valoarea de ieșire a obiectului de control, un model matematic este scris în forma normală Cauchy:
- ecuația valorii de ieșire a obiectului.
unde A, B, C, D sunt matrice, X este matricea variabilelor interne, U este matricea variabilelor de intrare, în acest caz U este EMF.
În acest caz, matricile vor arăta astfel:
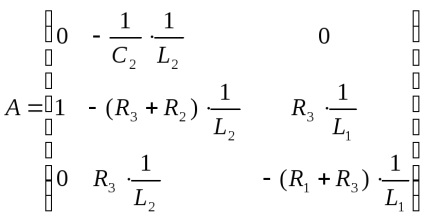
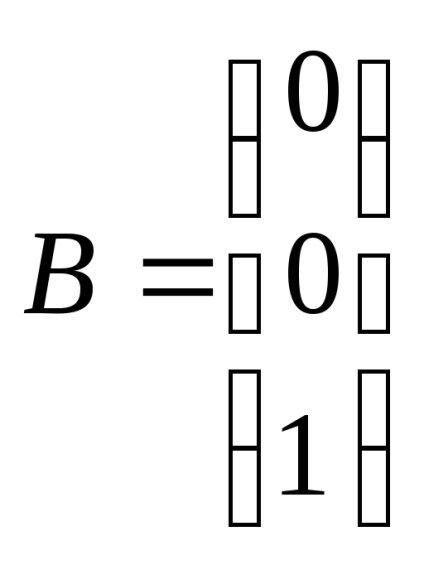
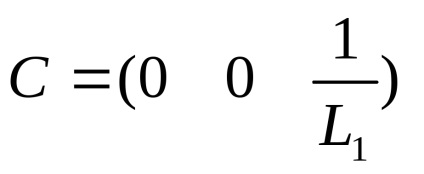
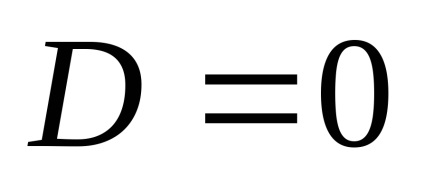
Obținem un model matematic în spațiul de stare: