Definiția trienței naturale a lui Frenet. Proiecții ale vitezei și accelerației unui punct pe axa sa. Un exemplu de determinare a ortelor unui triedron natural.
Pe „cinematicii punctului material“ pagina, am stabilit că vectorul de viteză al punctului este direcționat la o tangentă la calea. Vectorul de accelerație se află în planul învecinat și poate fi descompus în două componente. O componentă este îndreptată de-a lungul tangentei spre traiectorie. A doua componentă direcționată perpendicular pe tangenta la partea laterală a centrului instantaneu de curbură a traiectoriei.
În unele cazuri, este convenabil să se introducă un sistem de coordonate asociat poziției curente a punctului. Luați în considerare un punct la un moment dat. Credem că știm traiectoria mișcării sale. Tragem prin punctul trei linii - tangenta la traiectorie, principala normala si binormala. Principalul normal este perpendicular pe tangent și îndreptat spre centrul instantaneu de curbură al traiectoriei. Binormalul este perpendicular pe normalele tangente și principalele. Alegem un sistem de coordonate cu originea la punctul și axele direcționate de-a lungul acestor linii. Un astfel de sistem de coordonate se numește triedronul natural Frenet. Axele acestui sistem de coordonate sunt numite axele triedronului natural.
Orth a unui triedron natural
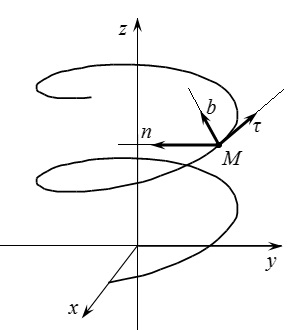
Lasă-l să fie. și sunt vectorii unității direcționați de-a lungul tangentei, principalul normal și binormal la traiectorie, respectiv. Acești vectori sunt vectorii unității sistemului de coordonate ales de noi sau ortele triedronului natural. Să analizăm problema alegerii direcției acestor vectori.
Vectorul este direcționat de-a lungul tangentei pe traiectorie. Prin urmare, puteți alege două direcții opuse. Cea mai convenabilă modalitate este de a indica de-a lungul vectorului de viteză al punctului. atunci
.
Cu toate acestea, acest lucru nu se poate face întotdeauna. Există cazuri în care traiectoria mișcării este cunoscută în avans, iar viteza nu este. De exemplu, atunci când un punct se deplasează de-a lungul unui jgheab în interiorul unui solid sub influența forțelor exterioare. În astfel de cazuri, direcția vectorului este aleasă în avans. De exemplu, în direcția creșterii coordonatelor de arc.
Direcția vectorului unității principalei normale este determinată în mod unic. Este direcționat perpendicular. în direcția centrului instantaneu de curbură a traiectoriei.
Vectorul binormal este direcționat perpendicular pe vectori și astfel încât cei trei vectori. și a format un sistem de coordonate drepte:
.
Viteza și accelerarea unui punct din triedronul Frenet
Presupunem că vectorul coincide în direcția vectorului de viteză al punctului. Apoi aplicăm formulele pe care le-am derivat pe pagina "Cinematica punctului material".
Adică într-un triedru natural cu orte. viteza are o componentă:
.
egală cu modulul de viteză. Cu alte cuvinte, modulul de viteză este proiecția vectorului de viteză pe axa triedronului natural. Proiecțiile vectorului de viteză pe axă și triedron sunt zero.
Accelerarea are două componente:
.
Aceste componente sunt accelerație tangențială și normală:
;
.
Adică accelerația tangențială și normală sunt proiecțiile vectorului de accelerare pe axă și triedronul natural. Proiecția vectorului de accelerare pe axă este zero.
Cum se determină axele unui triedron natural
Mai mult, credem că avem un sistem de coordonate fix. Punctul material se mișcă. Este necesar să găsiți axele unui triedron natural. Asta este, determinați proiecțiile unităților. și în sistemul de coordonate.
Pentru metode coordonate și vectoriale de specificare a mișcării
Pentru a coordona și metode de atribuire a vectorului punctului, formulele de determinare a vectorilor de bază prezentate în „punctul Cinematica materialul“ pagina. Pe pagina "Metoda coordonată pentru specificarea mișcării unui punct" este discutat un exemplu de calcul al componentelor vectorilor.
Adică, pentru a determina ortele triedronului natural, trebuie să găsim componentele vectorilor de viteză și accelerația normală. aplicând următoarele formule:
;
;
;
.
În continuare, definim vectorii unității triedronului natural:
;
;
.
Pentru un mod natural de a specifica mișcarea
În modul natural de a specifica mișcarea unui punct, știm traiectoria mișcării sale. Prin urmare, ne confruntăm cu sarcina - de-a lungul unei traiectorii cunoscute, de a determina ortele unui triedron natural. Dacă traiectoria este o figură geometrică simplă, de exemplu un cerc, atunci determinați vectorii. și poate fi geometric.
În general, și într-un caz mai complicat, este necesară reprezentarea ecuației de traiectorie într-o formă parametrică. Pentru aceasta, introduceți parametrul. Acest lucru se poate face în mai multe moduri. Prin urmare, este de dorit să alegeți cea mai convenabilă reprezentare.
Să presupunem, de exemplu, că traiectoria mișcării este o elipsă situată în avion.
.
Cea mai convenabilă reprezentare parametrică poate fi obținută dacă folosim formula trigonometrică:
.
Apoi ecuația traiectoriei are forma:
Aici este parametrul.
Aceasta nu este singura modalitate de a obține o reprezentare parametrică. Se poate rezolva, de exemplu, ecuația elipsei cu privire la.
.
Aplicând această formulă obținem o altă reprezentare parametrică:
Mai mult, presupunem că aceste ecuații parametrice descriu mișcarea unui punct material, în care parametrul joacă rolul timpului. Apoi, pentru a determina axele triedrului, putem aplica formulele folosite pentru vector și putem coordona metodele de specificare a mișcării. Viteza și accelerația calculate vor depinde de reprezentarea parametrică selectată. Dar caracteristicile geometrice ale traiectoriei, cum ar fi vectorii unitari. și raza de curbură a traiectoriei nu depind de reprezentarea parametrică selectată.
Așadar, pentru a găsi ortele unui trident natural pe o anumită traiectorie de mișcare. Este necesar să se reprezinte ecuația traiectoriei într-o formă parametrică și să se aplice formulele utilizate pentru metoda de coordonate de specificare a mișcării.
Un exemplu de determinare a ortelor unui triedron natural
Găsiți vectorii unitate de-a lungul axelor de triedru naturale, iar raza de curbură a traiectoriei, pentru o elice cilindrică, cu raza de bază și smoală.
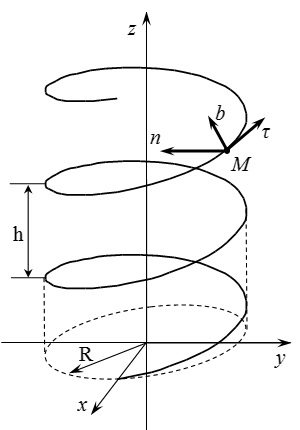
Alegem un sistem de coordonate. Axa este direcționată de-a lungul axei spiralei. Apoi, ecuația liniei poate fi reprezentată în următoarea formă parametrică:
(1)
Iată parametrul; Dacă luăm proiecția punctului liniei, în avion. atunci acesta este unghiul dintre axă și proiecție. Când creșteți cu. coordonatele și punctele se întorc în poziția lor inițială, iar coordonatele cresc cu.
Presupunem că ecuațiile (1) descriu mișcarea unui punct de-a lungul unei helixuri. Determinăm cantitățile cinematice pentru această mișcare.
Diferențierea ecuațiilor (1) în raport cu. găsim componentele vectorului de viteză:
;
;
.
Viteza pătrată:
.
Modul de viteză:
.
Un vector de unitate în direcția tangentei pe traiectorie:
.
Diferențierea componentelor vectorului de viteză în raport cu. găsim componentele vectorului de accelerare:
;
;
.
Accelerația tangențială este proiecția accelerației pe direcția vectorului.
Acest rezultat poate fi obținut într-un mod mai simplu. Pentru a face acest lucru, luăm în considerare faptul că modulul de viteză nu depinde de u și aplicăm formula:
.
Vector de accelerare tangențială:
.
Vectorul de accelerație normală:
Pătrat al vectorului accelerației normale:
.
Modulul vectorului accelerației normale:
.
Raza de curbură a traiectoriei:
.
Un vector de unitate în direcția normală a traiectoriei:
.
Un vector de unitate în direcția binormală: