Continuăm să ne pregătim pentru USE în domeniul informaticii și astăzi vom lua în calcul rezolvarea unor probleme cum ar fi A10.
Sarcinile de acest tip sunt destul de complicate. Abordarea soluției lor, fără a cunoaște elementele de bază ale logicii, nu merită. Prin urmare, vă recomand să citiți despre conjuncție. disjuncție. implicație.
Există două segmente pe linia numerică: P = [1, 39] și Q = [23, 58].
Alegeți dintre segmentele propuse un astfel de segment A ca expresia logică
(x ∈ P) → β (x ∈ Q)) → β (x ∈ A)
este identic adevărat, adică este nevoie de valoarea 1 pentru orice valoare de x.
1) [5, 20] 2) [25,35] 3) [40,55] 4) [20, 40]
Pentru comoditate, să menționăm simplele noastre afirmații cu majuscule latine (după numele segmentelor):
Rescriim expresia noastră într-o formă mai convenabilă:
Problema 10 a examenului de stat unificat în domeniul informaticii
Acum, o mică deviere față de implicare. Implicația poate fi exprimată prin disjuncție și negare în acest fel:
Dezvăluirea implicării prin disjuncție și negare
Aceasta este o regulă foarte importantă și trebuie amintită.
Acum ne putem rescrie afirmația, rămânând implicată:
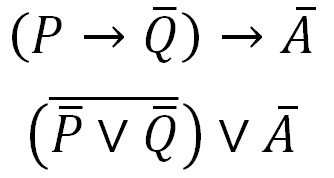
Pentru a simplifica expresia în paranteze, vom folosi legea de Morgan (cea de-a doua din imagine)
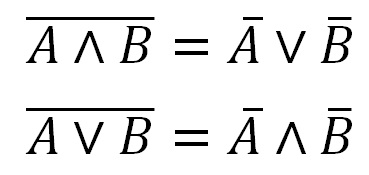
Legile lui de Morgan
Ca rezultat, ajungem
Aplicând legea dublei negări, obținem declarația finală cu care vom continua să lucrăm. Da, nu e tot
Acum, să ne amintim că declarațiile noastre sunt segmente și le afișăm pe linia de coordonate.
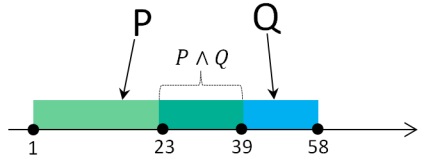
Programați pentru sarcină
Să analizăm graficul și declarația finală. Declarația finală trebuie să fie valabilă pentru orice valoare de x de condiția problemei. În declarația finală, expresia în paranteze și inversiunea A sunt legate prin disjuncție. Disjuncția este adevărată atunci când cel puțin una sau ambele afirmații sunt adevărate. Aceasta înseamnă că declarația finală va fi adevărată atunci când fie expresia în paranteze este adevărată, fie negarea lui A este adevărată, sau ambele expresii sunt adevărate (în paranteze și negarea lui A). Expresia în paranteze este o conjuncție și este adevărată numai atunci când ambele declarații sunt adevărate. Asta este, atunci când x aparține intervalului [23, 39], afirmația finală este adevărată. În caz contrar, declarația va fi falsă și apoi negarea A ar trebui să fie adevărată. Vom lua în considerare când va fi așa.
La inceput, am stabilit ca declaratia A inseamna ca x ∈ A. Deoarece este cu noi cu negare, negarea lui A va insemna ca x ∉ A, deci punctul x trebuie sa apartina intervalului [-∞, 23] sau [39 , + ∞]. Rămâne să găsim un astfel de segment A, care se va suprapune intervalului [23, 39] (de vreme ce îl avem cu un negativ, apoi în final ajungem la intervalul de care avem nevoie). Adică coordonatele din stânga ale segmentului trebuie să fie mai mari sau egale cu 23, iar cea dreaptă este mai mică sau egală cu 39.
Dintre opțiunile propuse, numai [25, 35] este adecvată. Răspunsul corect este 2.
Un alt exemplu de rezolvare a sarcinii A10 EGE în informatică (la cererea Eugenia).
Pe linia numerică sunt date trei segmente:
P = [0,40], Q = [20,45] și R = [10,50].
Alegeți un segment A astfel încât formula ((x∈P) → (x∈Q)) ∨ ((x∉A) → (x∉R)) să fie identică, adică să ia valoarea 1 pentru orice valoare de x.
1) [5,20] 2) [10,15] 3) [15,20] 4) [35,50]
Pentru comoditate, luăm următoarea notație:
Acum putem rescrie formula noastră în această formă:
Aplicând legea lui Morgan, obținem următoarele:
Pentru comoditate, să denotăm expresii în paranteze cum ar fi:
Rămâne să afișați formula pe linia de număr.
Luați în considerare expresia Z și transferați-o la o linie numerică
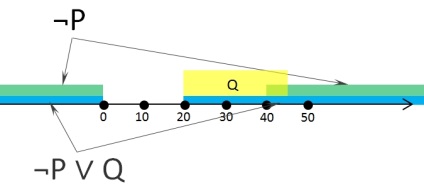
Aici avem o culoare verde pentru regiunea ¬P, galben pentru Q, și albastru pentru ¬P ∨ Q.
Acum observăm că expresiile din paranteze sunt unite prin disjuncție. ceea ce înseamnă că expresia finală va fi identică când cel puțin una sau ambele expresii din paranteze sunt adevărate simultan.
Acum vedem că dacă variabila x aparține domeniului [-∞; 0] sau [40; + ∞], atunci expresia finală va fi adevărată.
Considerăm a doua expresie A ∨ ¬R (am șters regiunile ¬P și Q din figura precedentă, astfel încât să nu interfereze, lăsând doar domeniul finit ¬P ∨ Q):
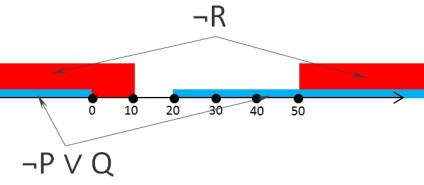
Soluția sarcinii A10 EGE în informatică
După cum puteți vedea, expresia din al doilea bracket va fi adevărată numai atunci când x aparține domeniului [-∞; 10] sau [50; + ∞]. Expresia generală va fi adevărată atunci când x aparține domeniului [-∞; 10] sau [20; + ∞].
Dar dacă x este în intervalul (10; 20), atunci expresia finală va fi falsă. Așadar, trebuie să găsim o valoare a intervalului A, care va suprapune intervalul (10; 20). Din condițiile propuse în condiție, numai această gamă [5.20] îndeplinește această condiție.