Capitolul 2. Soluții și sisteme de dispersie
EXEMPLUL 2.7. Ce volum de soluție de acid clorhidric cu o fracție de masă de 36% și o densitate de 1,179 g / ml este necesar pentru a produce 250 ml dintr-o soluție de acid clorhidric cu o concentrație molară de 0,1 mol / l?
Soluție Conform formulei (2.1), transformată în raport cu n (X), găsim cantitatea de substanță clorhidrică necesară pentru prepararea soluției cerute:
l (HC1) = soluție c (HC1) K = 0,1 mol / l-0,25 litri = 0,025 mol.
Masa corespunzătoare acestei cantități de substanță se calculează prin formula (2.2), transformată în raport cu m (X) '
/ H (HCI) = "(HCI) M / (HCI) = 0,025 moli 36,5 g / mol = 0,9125 g.
Aceeași masă de acid clorhidric trebuie inclusă în soluția inițială. Găsim masa acestei soluții prin formula (2.4), transformată cu respect
t (HCI) 0,9125 g.
/ "soluția, totalul GT7 4, JJ4 G.
Volumul necesar al soluției este calculat prin formula
unde p din soluție este densitatea soluției Înlocuind în această formulă valoarea calculată a masei soluției și a densității soluției,
soluția indicată în problemă
^ soluție = 2,535 G 1,179 G / ML = 2,15 ML.
Solubilitatea solidelor și lichidelor se caracterizează prin coeficientul de solubilitate, care indică cât de mult din substanță se poate dizolva cât mai mult posibil în 100 g de solvent. Coeficientul de solubilitate este deseori pur și simplu numit solubilitate. O soluție în care substanța nu se mai poate dizolva la o anumită temperatură se numește saturată
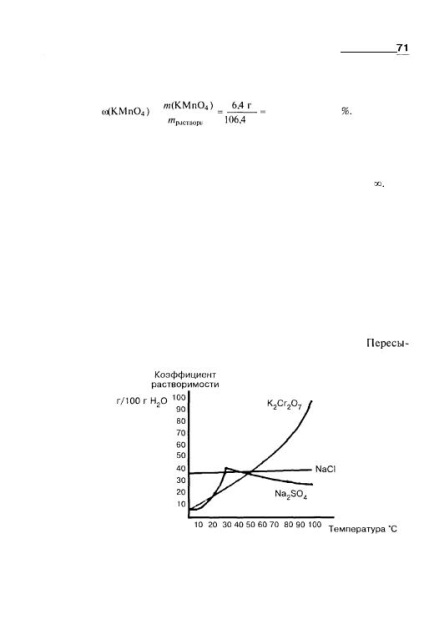
EXEMPLUL 2.8. Coeficientul de solubilitate al permanganatului de potasiu la 20 ° C este de 6,4 g. Se calculează fracția de masă a permanganatului de potasiu în soluția sa saturată la această temperatură
Soluția. Să presupunem că masa de permanganat de potasiu dizolvat este de 6,4 g. Apoi, pe baza determinării coeficientului de solubilitate, masa apei este de 100 g, iar masa soluției este suma substanței dizolvate și a solventului:
/ "soluție = /" (KMnO4) + / n (H20) = 6,4 g + 100 g = 106,4 g.
2.3. Metode de exprimare cantitativă a compoziției soluției
Fracțiunea de masă a permanganatului de potasiu într-o soluție saturată în conformitate cu formula (2.4) este egală cu:
Unele lichide sunt amestecate în orice raport, de exemplu, etanol, glicerină, acetic Acid. Necondiționata dizolvare este marcată de simbolul oo. Solubilitatea lichidelor dizolvate în mod limitat crește, de regulă, cu creșterea temperaturii. Atunci când se atinge o anumită valoare, solubilitatea poate deveni nerestricționată. De exemplu, la 16 ° C, 6,7 g de fenol se dizolvă în 100 g de apă, dar la o temperatură peste 66 ° C se amestecă fenolul cu apă în orice raport. De asemenea, solubilitatea solidelor crește, în general, cu creșterea temperaturii. Figura 2.3 prezintă natura diferită a efectului temperaturii asupra solubilității anumitor săruri. Dacă soluția saturată la o temperatură mai ridicată este răcită cu grijă, se poate obține o soluție suprasaturată, fracția de masă a substanței dizolvate în care este mai mare decât fracția de masă calculată utilizând factorul de solubilitate. suprasaturație Fig. 2.3. Dependența solubilității anumitor săruri la temperatură: solubilitatea dicromatului de potasiu crește brusc cu creșterea temperaturii; solubilitatea clorurii de sodiu variază nesemnificativ, rămânând practic constantă; solubilitatea sulfatului de sodiu crește mai întâi și apoi scade.
Substanțele cu legături covalente ionice sau puternic polare în soluții apoase sunt supuse disocierii electrolitice, rezultând formarea de cationi ionici și anioni încărcați opus. Cationii au o încărcătură pozitivă și se deplasează într-un câmp electric extern la catod, anionii sunt încărcați negativ, se deplasează la anod. Soluțiile care conțin ioni sunt capabile să efectueze electricitate. Topiturile de compuși ionici sunt, de asemenea, capabili să conducă electricitate. Soluțiile și topiturile care conțin ioni se numesc conductori de electricitate de tipul celui de-al doilea tip (metalele primului tip se numesc conductori de primul fel, în care electronii sunt purtători de energie electrică). Electroliții sunt substanțe capabile să formeze conductori de tipul celui de-al doilea. Electroliții sunt, de asemenea, numiți soluții și topituri care conțin ioni. Electroliții sunt practic toate sărurile, acizii și bazele. Teoria disocierii electrolitice a fost propusă în 1887 de fizicianul suedez S. Arrhenius.
Substanțele cu legături covalente slabe polare și nepolare, incapabile de disociere electrolitică, sunt numite non-electroliți. Acestea includ toate substanțele simple, hidrocarburile, alte substanțe organice. Abilitatea substanțelor moleculare la disocierea electrolitică nu caracterizează o substanță individuală, ci un sistem - o substanță dizolvată + un solvent. De exemplu, etanolul C2H5OH în apă nu este electrolit și în amoniac lichid este un electrolit. Clorura de hidrogen în soluție apoasă este electrolit și în soluție de benzen - non-electrolitic. Deoarece soluțiile apoase au cea mai mare valoare în viața noastră, în acest capitol ne limităm la soluții în care solventul este apa.
Electroliții, la rândul lor, sunt împărțiți în puternici, medii și slabi. Electroliții puternici sunt capabili să disocieze complet: aceasta înseamnă că substanța în soluție există practic doar în formă ionică. Electroliții puternici includ majoritatea substanțelor din compoziția ionică, adică sărurile, precum și unele substanțe cu structură moleculară, de exemplu, HCI. Electroliții slabi disociază nesemnificativ, iar forma predominantă a existenței lor în soluție este moleculară. Electroliții cu rezistență medie se disociază în așa fel încât concentrația de ioni și molecule în soluțiile lor să fie comparabilă.
Capitolul 2. Soluții și sisteme de dispersie
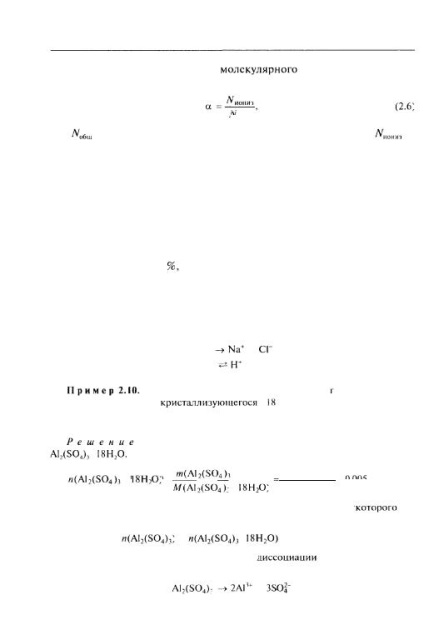
Din punct de vedere cantitativ, capacitatea unui discontinuu de electrolit molecular este determinata de gradul de ionizare (a):
unde N este numărul total de molecule în soluție; N Hmm este numărul de molecule care se descompun în ioni.
Gradul de ionizare este exprimat în fracțiuni ale unei unități sau în procente. Gradul de disociere de 0,01 sau 1% înseamnă că din cele 100 de molecule ale substanței dizolvate, numai unul sa descompus în ioni. Așa cum se va arăta în capitolul 9, gradul de disociere depinde de concentrația electrolitului; crește cu scăderea concentrației. Prin urmare, este posibilă compararea electroliților între ei în ceea ce privește gradul de ionizare numai la o anumită concentrație de electroliți. Dacă gradul de ionizare a electrolitului într-o soluție cu o concentrație molară de 0,1 mol / l este mai mare de 30%, atunci este considerat puternic dacă mai puțin de 3% este slab. Electroliții, pentru care gradul de ionizare la această concentrație este în gol, sunt considerați medii.
Ecuațiile de disociere electrolitică sunt scrise ca ecuații de reacții obișnuite, pentru electroliți puternici - cu săgeată unilaterală, pentru mediu și slab - cu două fețe, de exemplu:
EXEMPLUL 2.10. Într-o cantitate de 500 ml apă, 3,33 g hidrat de cristal de sulfat de aluminiu cristalizează cu 18 molecule de apă. Se calculează concentrația molară a fiecărui ion în soluția rezultată. Schimbarea volumului în timpul dizolvării este neglijată.
Soluția. Unitatea acestui hidrat cristalin este A1 2 (SO 4) 3 - 18H 2 O. Să ne găsim cantitatea prin formula (2.2):
Cantitatea de material de sulfat de aluminiu, la disocierea căreia se formează ioni, este egală cu cantitatea de hidrat de cristal:
"(A1 2 (SO4) 3) = n (A1 2 (8O4) 3-18 H20) = 0,005 mol.
Să notăm ecuația disocierii electrolitice a sulfatului de aluminiu, având în vedere că această substanță, ca majoritatea sărurilor, este un electrolit puternic:
A1, (SO4), -> 2A1 1+ + 3SO4

2.4. Disocierea electrolitică
După cum rezultă din ecuația de mai sus,
l (A1 +) = 2n (Al2 (8O4), / i (SOj
După înlocuirea cantității de material de sulfat de aluminiu, obținem:
l (A1 3+) = 2-0,005 = 0,01 mol; (S0 ^
) = 3-0,005 = 0,015 mol.
Dacă se folosește formula (2.1), este posibil să se calculeze concentrațiile moleculare ale ambelor ioni în soluție:
EXEMPLUL 2.11. Unele volume de soluție de amoniac conțin 1,814 mmoli de molecule de amoniac și 0,186 mmoli de ioni de amoniu. Calculați gradul de ionizare a amoniacului în această soluție.
Soluția. Să notăm ecuația de disociere electrolitică a amoniacului, ținând seama de faptul că acesta este un electrolit slab:
N H 3 + H 2 O * ± NO + OFT.
În conformitate cu ecuația de mai sus, cantitatea de substanță amoniac supusă ionizării (ion ion) este egală cu cantitatea de substanță ion de amoniu:
w (NH3) m> H Hj = "(NHJ) = 0,186 mmol.
Cantitatea totală de amoniac din soluție este egală cu suma cantităților de amoniac ionizat și amoniac sub formă moleculară:
n (MH3) total = n (MH3) ion + + (NH3) 40 ^ KW = 0,186 mmol + 1,814 mmol = 2 mmol.
În conformitate cu formula (2.6), gradul de ionizare a amoniacului în această soluție este:
a = nCNHaUHH. = 86 mmoli = Q / J93 ^ 9> 3% (NH3) = 2 mmoli

Capitolul 2. Soluții și sisteme de dispersie
2.5. Vederi generale
pe sisteme de dispersie
După o cunoaștere preliminară cu proprietățile soluțiilor, să analizăm pe scurt câteva proprietăți ale sistemelor dispersate. Sistemele de dispersie heterogene sunt împărțite în sisteme cu dispersie înaltă (mărimea particulelor în intervalul de 10 ° C)
7 m) și sisteme dispersate cu grosime (dimensiunea particulelor în intervalul 10 -
5 m). Agregatul de particule sfărâmate în sistemele dispersate se numește faza de dispersie, iar mediul în care sunt distribuite particulele dezintegrate este un mediu de dispersie.
Exemple de sisteme dispersate cu aspru sunt suspensiile și emulsiile. În suspensii, particulele unei substanțe solide (faza dispersată) sunt dispersate într-un mediu de dispersie lichidă. Sistemul de dispersie, în care particulele de sulfat de calciu solid sunt distribuite în apă, este un exemplu de suspensie. O astfel de suspensie este folosită, de exemplu, pentru tencuielile pereților și pentru a face artefacte (alabastru), precum și pentru a realiza pansamente de gips în medicină. Emulsie - un tip grosier de sistem în care picături mici dintr-un lichid (faza dispersată) este dispersată într-un mediu de dispersie lichid. Un exemplu clasic de emulsie este laptele, în care picături de grăsime sunt dispersate într-o soluție apoasă de săruri și proteine.
Sistemele superfine, denumite și sisteme de dispersie coloidală sau soluri, ocupă o poziție intermediară între soluțiile reale și sistemele cu dispersie grosieră. Acestea, de exemplu, ca soluții reale, trec printr-un filtru normal, în timp ce particulele de sisteme dispersate grosier cu un astfel de filtru sunt întârziate. Sistemele coloid-dispersate, precum și sistemele dispersate prea gros, sunt stratificate. Pentru sistemele de dispersie coloidală, opalescenta este caracteristică, care este evaluată subiectiv ca o stare intermediară între o soluție limpede și o suspensie turbidă. Dacă luăm în considerare un sol plasat într-un tub de laborator, pe o parte, adică în lumină transmisă, se va crea o impresie de transparență a sistemului. Dacă luăm în considerare același sol în lumina reflectată, adică, privim în tubul de sus în jos, se va crea impresia de turbiditate a sistemului. Dacă trimiteți un fascicul de lumină subțire la sol, puteți vedea urmele de lumină care trec prin cenușă sub forma unui con luminos (conul Tyndall) (Figura 2.4).
Sistemele dispersate coloidală joacă un rol imens în viața umană. Practic toate țesuturile de plante și animale
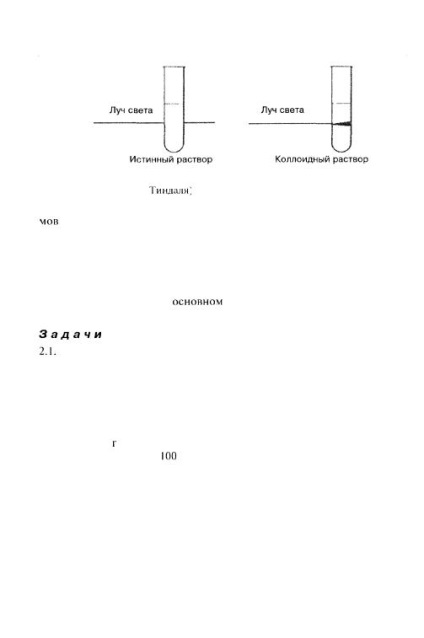
Fig. 2.4. Atunci când un fascicul de lumină trece printr-o soluție coloidală, un con luminos (conul Tyndall)
sunt sisteme dispersate coloidale. Acestea includ unele medicamente, multe produse alimentare, precum și materiale utilizate în industrie și acasă.
Dispozitivele de dispersie, în care mediul de dispersie este un gaz, se numesc aerosoli. Fumul, ceața, smogul sunt exemple de aerosoli.
Proprietățile soluțiilor (vezi Capitolul 9) și sistemele de dispersie (vezi capitolul 20) sunt dezasamblate temeinic în cursul principal.
2.1. Etanol, cântărind 90 g, a fost dizolvat în 410 g de apă. Se calculează fracția de masă de alcool din soluția rezultată.
2.2. Se calculează masa de hidroxid de sodiu conținut în 1,2 kg soluție de 7,5%.
2.3. Se calculează masa de apă conținută în 170 g dintr-o soluție de clorură de potasiu de 10%.
2.4. Se calculează masa unei soluții de azotat de potasiu de 19%, care conține 95 g din această sare.
2.5. La o soluție de 100 g de masă cu o fracție de masă de acid sulfuric de 24% s-au adăugat 300 g de apă. Calculați fracția de masă a acidului în noua soluție.
2.6. La o soluție de 200 g de masă cu o fracție de masă de hidroxid de potasiu de 25% s-au adăugat 50 g aceiași alcalii. Se calculează fracția de masă a substanțelor alcaline în noua soluție.
2.7. Dintr-o soluție de 500 g cu o fracție de masă de azotat de litiu de 4%, se evaporă 300 g de apă. Calculați fracția de masă a sării în noua soluție.
2.8. Din o soluție cântărind 250 g cu o fracție de masă de clorură de magneziu de 40%, 50 g din această sare cristalizează. Calculați fracția de masă a sării în noua soluție.

Capitolul 2. Soluții și sisteme de dispersie
2.9. S-a dizolvat acid sulfuric cu greutate de 14,7 g în apă și volumul soluției a fost adus la 200 ml. Se calculează concentrația molară a acidului în soluția rezultată.
2.10. Care este masa de dicromat de potasiu necesar pentru a prepara o soluție de 0,75 litri cu o concentrație molară de 0,2 mol / l?
2.11. În ce volum de soluție cu concentrația molară de clorură de bariu 0,12 moli / l conține 6,24 g din această sare?
2.12. Se dizolvă sulfat de amoniu de 45 g în 180 g de apă și se obține o soluție cu o densitate de 1,115 g / ml. Se calculează concentrația de masă a sării în soluție.
2.13. Se calculează masa unei soluții de sare cu o fracție de masă de 5% pentru a prepara 100 g dintr-o soluție din aceeași sare cu o fracție de masă egală cu 2%.
2.14. Se calculează masa soluției de sare cu o fracție de masă de 10%
ar trebui luată pentru a prepara 1 kg de soluție din aceeași sare cu o fracție de masă egală cu 8%.
2.15. Calculați cantitatea de apă adăugată la 0,5 kg de soluție sărată cu o fracție de masă de 20% pentru a obține o soluție din aceeași sare
cu o fracție de masă egală cu 15%.
2.16. Calculați cantitatea de apă adăugată la o soluție de sare cu o fracție de masă de 20% pentru a obține 0,5 kg de soluție de aceeași sare
cu o fracție de masă egală cu 15%.
2.17. Se calculează concentrația molară a soluției de clorură de glică (II) cu o fracție de masă egală cu 10% (1,022 g / ml).
2.18. Se calculează concentrația molară a soluției de sulfat de cupru cu o fracție de masă egală cu 0,12 (1,131 g / ml).
2.19. Se calculează concentrația molară a unei soluții de azotat de crom (III) cu o fracție de masă egală cu 16% (1,141 g / ml).
2.20. Se calculează concentrația molară a soluției de bromură de cobalt (II) cu o fracție de masă egală cu 0,18 (1,182 g / ml).
2.21. Se calculează fracția de masă a acidului azotic în soluție cu o concentrație molară egală cu 6,273 mol / l (1,200 g / ml).
2.22. Se calculează fracțiunea de masă de acid sulfuric în soluție cu o concentrație molară egală cu 0,1783 mol / l (1,010 g / ml).
2.23. Se calculează fracțiunea de masă de acid clorhidric în soluție cu o concentrație molară egală cu 1,20 mol / l (1,025 g / ml).
2,24. Se calculează fracția de masă a acidului fosforic în soluție cu o concentrație molară egală cu 1,510 mol / l (pl., 1,075 g / ml).
2.25. Calculați cât de mult soluție de clorură de aluminiu, cu o fracție de masă de 0,16 (pl. 1,149 g / ml) necesară pentru a prepara 500 ml dintr-o soluție cu o concentrație molară de 0,1 mol / l.
